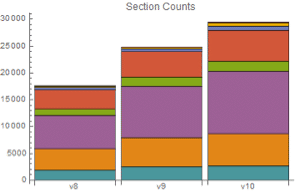
Fractional Gaussian Noise versus FARIMA Noise
A FARIMAProcess with no autoregressive and no moving-average components and a discrete time restriction of a FractionalGaussianNoiseProcess are frequently used to model colored noises.
| In[1]:= | X |
| In[2]:= | X |
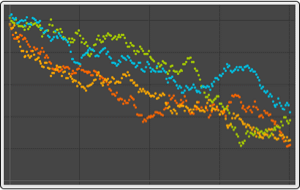
Simulate both processes for integer times.
| In[3]:= |  X |
FractionalGaussianNoiseProcess simulation.
| In[4]:= | X |
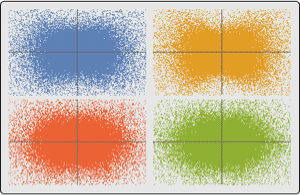
| Out[4]= |  |
| In[5]:= | X |
| Out[5]= | 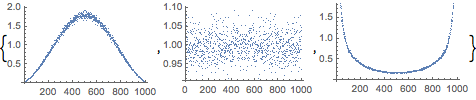 |
FARIMA noise simulation.
| In[6]:= | X |
| Out[6]= |  |
| In[7]:= | X |
| Out[7]= | 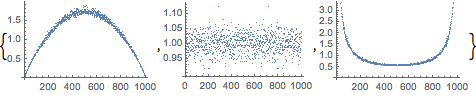 |
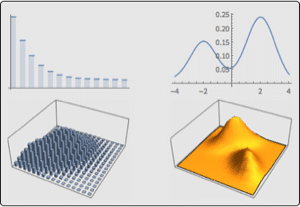
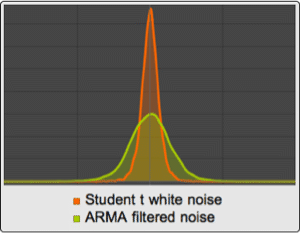
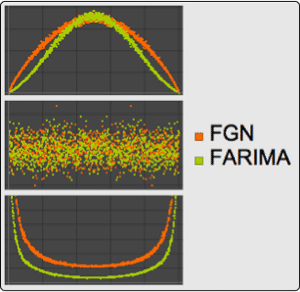
Compare periodogram plots.
| Out[8]= | 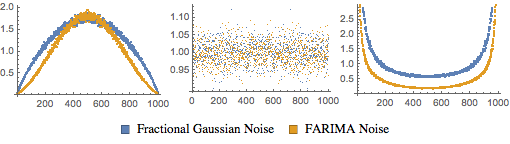 |