Perform Typo Correction without a Dictionary
Modeling the sequence of typed characters as observations and the sequence of the correct characters as hidden states, this example uses two different models for the evolution of correct letters to correct for typos. The first model uses the first-order Markov process to encode frequencies of what follows the given character. The second model uses the second-order Markov states to encode frequencies of what follows the given last two characters.
Take Darwin’s The Origin of Species and convert all non-letter symbols to spaces.
| In[1]:= |  X |
| In[2]:= | X |
Introduce typos, at a 20% rate, by randomly replacing a character with one of its immediate neighbors on the standard QWERTY keyboard. The space character is never mistyped.
| In[4]:= |  X |
| In[5]:= |  X |
| Out[6]= | 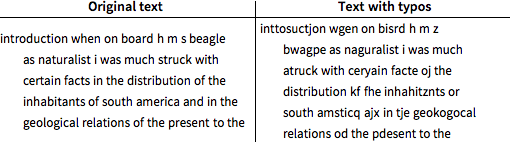 |
Take the first 80,000 characters to be a test sequence, and the remainder of the text as a training sequence. The test sequence has 16.5% mistyped characters, less than 20% because the space character was never mistyped.
| In[7]:= |  X |
| Out[7]= |
Model the stream of typed characters using hidden Markov process. Correct characters are hidden states, while the actual typed characters are observations.
| In[8]:= |  X |
Estimate the hidden Markov process using training data.
| In[9]:= |  X |
| Out[9]= |
| In[10]:= |  X |
Use posterior decoding to correct typos in the test portion of the mistyped text.
| In[11]:= |  X |
| Out[11]= |
Corrected text still has 11% typos, 5.5% fewer than the original typed text.
| Out[12]= | 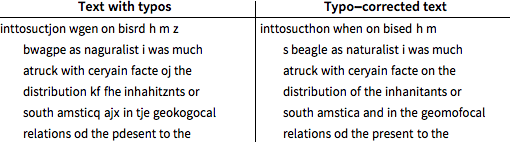 |
| In[13]:= |  X |
| Out[13]= |
Model evolution of the hidden states using a second-order Markov process; i.e. assume the probability of the character depends only on the two preceding characters. The second-order Markov process is modeled as a first-order Markov process with enlarged state space of pairs of consecutive characters.
| In[14]:= |  X |
| In[15]:= | 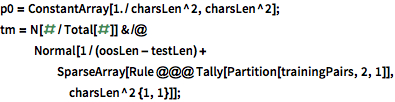 X |
The probability of the actual typed character depends only on the underlying true character.
| In[16]:= | X |
Repeat posterior decoding with the higher-order hidden Markov model.
| In[17]:= |  X |
| Out[17]= |
The percentage of typos has now been reduced to under 6%.
| In[18]:= |  X |
| Out[18]= |
| Out[19]= | 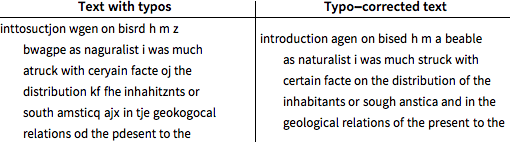 |