Hidden Markov Processes with Discrete or Continuous, Univariate or Multivariate Emissions
Define the initial probabilities and the conditional transition probabilities for the hidden states' dynamics.
| In[1]:= | X |
Define hidden Markov process with categorical emissions.
| In[2]:= | X |
 |
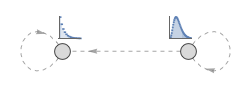
Define hidden Markov process with general discrete emissions.
| In[3]:= | X |
 |
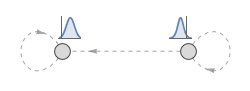
Define hidden Markov process with continuous emissions.
| In[4]:= | X |
 |
Define hidden Markov processes with multivariate emissions.
| In[5]:= |  X |
 |
| In[6]:= |  X |
 |
Sample each hidden Markov process.
| In[7]:= | X |
| In[8]:= | X |
Compute log‐likelihood of each path for the respective process.
| In[9]:= | X |
| Out[9]= |
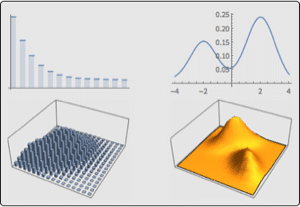
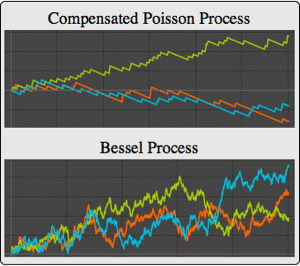
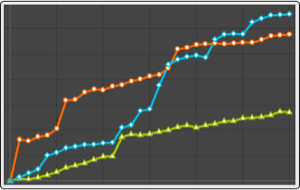
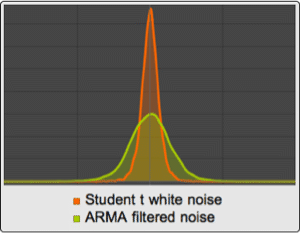
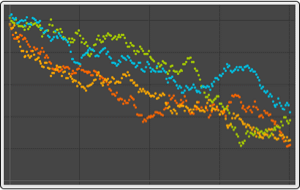
Visualize sample paths of processes with univariate emissions.
| Out[10]= | 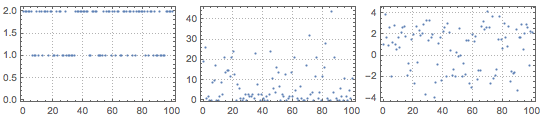 |
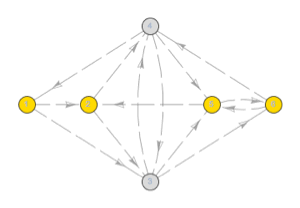
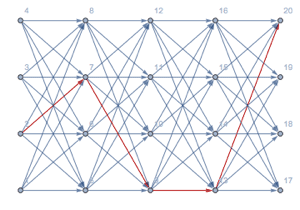
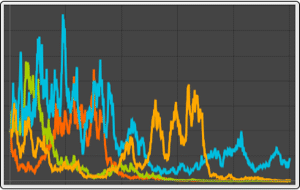
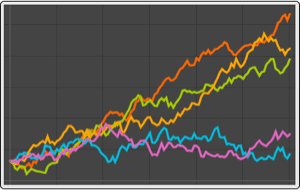
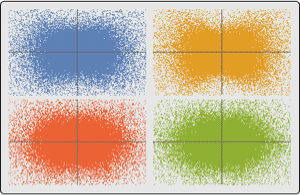
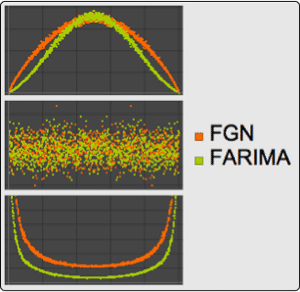
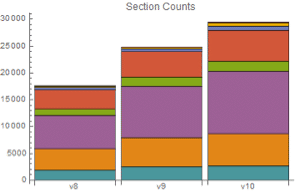
Visualize components of sample paths of processes with multivariate emissions.
| Out[12]= | 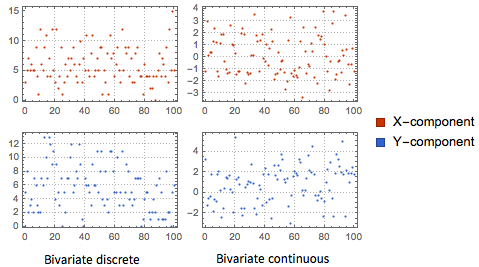 |