Использование разложения Смита для анализа решётки

Допустим, что решётка 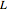была генерирована числами, кратными векторам 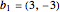и .

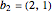In[1]:=

b1 = {3, -3}; b2 = {2, 1};

In[2]:=

ptsb = Flatten[Table[j b1 + k b2, {j, -12, 12}, {k, -12, 12}], 1];

In[3]:=

graphicsb = Graphics[{Blue, PointSize[Large], Point@ptsb}, PlotRange -> 10, Axes -> True]

Out[3]=

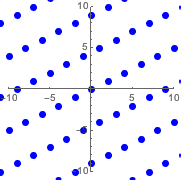
Допустим, что 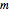является матрицей, чьи ряды - это 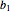и .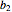

In[4]:=

m = {b1, b2};

Разложение Смита выдаёт три матрицы, удовлетворяющие тождеству .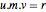

In[5]:=

{u, r, v} = SmithDecomposition[m];

In[6]:=

u.m.v == r

Out[6]=

Матрицы 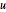и 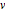имеют элементы целых чисел и одну детерминанту.

In[7]:=

{u // MatrixForm, v // MatrixForm, Det[u], Det[v]}

Out[7]=

Матрица 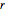- это целое число и диагональ. Исходя из её элементов, можно увидеть, что структура группы 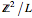- это 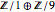или просто 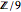, так как 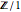является тривиальной группой.

In[8]:=

r // MatrixForm

Out[8]//MatrixForm=

Умножение правой части тождеств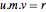а на 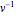производит 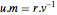. Так как 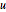является целым числом и детерминантой 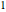, 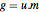генерирует такую же решётку как 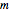, но только проще.

In[9]:=

g = r.Inverse[v]; g // MatrixForm

Out[9]//MatrixForm=

Визуализировать решётку, сгенерированную рядами .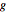

In[10]:=

ptsg = Flatten[ Table[j First[g] + k Last[g], {j, -12, 12}, {k, -12, 12}], 1];

In[11]:=

graphicsg = Graphics[{Red, PointSize[Medium], Point@ptsg}, PlotRange -> 10, Axes -> True]

Out[11]=

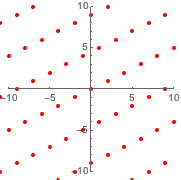
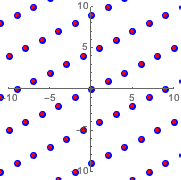
Наложение новой решётки на оригинальную доказывает, что они одинаковы.

In[12]:=

Show[{graphicsb, graphicsg}]

Out[12]=