使用史密斯分解分析晶格
考虑通过向量 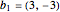 和
和 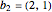 的整数倍产生的晶格
的整数倍产生的晶格 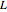 .
.
In[1]:=
b1 = {3, -3};
b2 = {2, 1};In[2]:=
ptsb = Flatten[Table[j b1 + k b2, {j, -12, 12}, {k, -12, 12}], 1];In[3]:=
graphicsb =
Graphics[{Blue, PointSize[Large], Point@ptsb}, PlotRange -> 10,
Axes -> True]Out[3]=
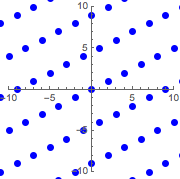
以 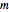 作为矩阵,其中行为
作为矩阵,其中行为 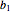 和
和 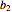 .
.
In[4]:=
m = {b1, b2};史密斯分解给出三个满足恒等式 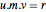 的矩阵.
的矩阵.
In[5]:=
{u, r, v} = SmithDecomposition[m];In[6]:=
u.m.v == rOut[6]=
矩阵 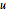 和
和 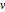 的项为整数,行列式为 1.
的项为整数,行列式为 1.
In[7]:=
{u // MatrixForm, v // MatrixForm, Det[u], Det[v]}Out[7]=
矩阵 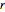 为整数矩阵且为对角矩阵. 从其项来看,可以发现
为整数矩阵且为对角矩阵. 从其项来看,可以发现 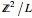 群的结构为
群的结构为 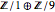 ,或直接写为
,或直接写为 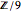 ,因为
,因为 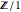 是平凡群.
是平凡群.
In[8]:=
r // MatrixFormOut[8]//MatrixForm=
恒等式 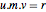 的右边乘以
的右边乘以 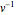 ,得出
,得出 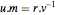 . 由于
. 由于 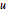 是整数矩阵且其行列式为
是整数矩阵且其行列式为 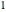 ,
,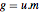 生成的是与
生成的是与 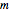 相同的晶格但更简单.
相同的晶格但更简单.
In[9]:=
g = r.Inverse[v];
g // MatrixFormOut[9]//MatrixForm=
可视化由 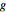 行生成的晶格.
行生成的晶格.
In[10]:=
ptsg = Flatten[
Table[j First[g] + k Last[g], {j, -12, 12}, {k, -12, 12}], 1];In[11]:=
graphicsg =
Graphics[{Red, PointSize[Medium], Point@ptsg}, PlotRange -> 10,
Axes -> True]Out[11]=
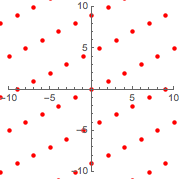
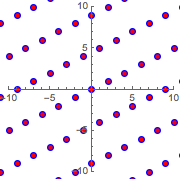
将新晶格与原来的晶格叠加确认它们是相同的.
In[12]:=
Show[{graphicsb, graphicsg}]Out[12]=