Wolfram Language™

Analysieren Sie einen Gittergraphen mit der Smith-Zerlegung

Untersuchen Sie den Gittergraphen 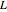, der von den ganzzahligen Vielfachen der Vektoren 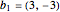und 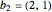generiert wird.

In[1]:=

b1 = {3, -3}; b2 = {2, 1};

In[2]:=

ptsb = Flatten[Table[j b1 + k b2, {j, -12, 12}, {k, -12, 12}], 1];

In[3]:=

graphicsb = Graphics[{Blue, PointSize[Large], Point@ptsb}, PlotRange -> 10, Axes -> True]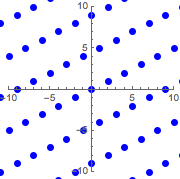

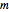Out[3]=

sei die Matrix mit den Zeilen 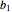und .

In[4]:=

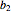m = {b1, b2};

Durch die Smith-Zerlegung ergeben sich drei Matritzen, die der Identität 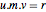genügen.

In[5]:=

{u, r, v} = SmithDecomposition[m];

In[6]:=

u.m.v == r

Out[6]=

Die Matritzen 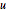und 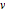haben ganzzahlige Einträge und eine Determinante gleich eins.

In[7]:=

{u // MatrixForm, v // MatrixForm, Det[u], Det[v]}

Out[7]=

Die Matrix 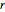ist ganzzahlig und diagonal. Aus den Matrixeinträgen ist ersichtlich, dass 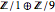oder einfach 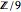die Struktur der Gruppe 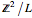ist, da 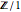die triviale Gruppe ist.

In[8]:=

r // MatrixForm

Out[8]//MatrixForm=

Multipliziert man die Identität 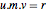auf der rechten Seite mal 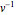, ergibt sich 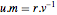. Da 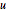ganzzahlige Einträge und die Determinante 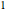hat, generiert 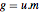dieselbe Gittergraphik wie 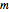, jedoch in einfacherer Ausführung.

In[9]:=

g = r.Inverse[v]; g // MatrixForm

Out[9]//MatrixForm=

Visualisieren Sie die Gittergraphik, die durch die Zeilen von 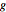generiert wurde.

In[10]:=

ptsg = Flatten[ Table[j First[g] + k Last[g], {j, -12, 12}, {k, -12, 12}], 1];

In[11]:=

graphicsg = Graphics[{Red, PointSize[Medium], Point@ptsg}, PlotRange -> 10, Axes -> True]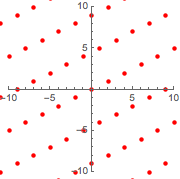

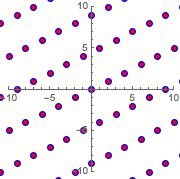
Out[11]=

Wenn Sie die neue Gittergraphik über das ursprüngliche Gitter legen, können Sie feststellen, dass die beiden gleich sind.

In[12]:=

Show[{graphicsb, graphicsg}]

Out[12]=