Uso de la descomposición de Smith para analizar un retículo
Considere el retículo 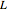 generado por números enteros múltiples de los vectores
generado por números enteros múltiples de los vectores 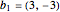 y
y 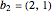 .
.
In[1]:=
b1 = {3, -3};
b2 = {2, 1};In[2]:=
ptsb = Flatten[Table[j b1 + k b2, {j, -12, 12}, {k, -12, 12}], 1];In[3]:=
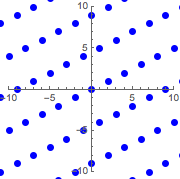
graphicsb =
Graphics[{Blue, PointSize[Large], Point@ptsb}, PlotRange -> 10,
Axes -> True]Out[3]=
Permita que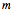 sea la matriz cuyas filas son
sea la matriz cuyas filas son 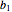 y
y 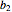 .
.
In[4]:=
m = {b1, b2};La descomposición de Smith proporciona tres matrices que satisfacen la identidad 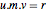 .
.
In[5]:=
{u, r, v} = SmithDecomposition[m];In[6]:=
u.m.v == rOut[6]=
Las matrices 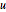 y
y 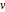 poseen entradas de números enteros y un factor determinante.
poseen entradas de números enteros y un factor determinante.
In[7]:=
{u // MatrixForm, v // MatrixForm, Det[u], Det[v]}Out[7]=
La matriz 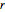 es una número entero y diagonal. A partir de sus entradas se puede ver que la estructura del grupo
es una número entero y diagonal. A partir de sus entradas se puede ver que la estructura del grupo 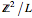 es
es 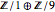 o simplemente
o simplemente 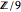 , en tanto
, en tanto 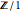 es el grupo trivial.
es el grupo trivial.
In[8]:=
r // MatrixFormOut[8]//MatrixForm=
Multiplicar la identidad 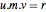 a la derecha por
a la derecha por 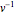 da
da 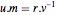 . Debido a que
. Debido a que 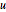 es un número entero y factor determinante
es un número entero y factor determinante 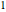 ,
, 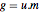 genera el mismo retículo como
genera el mismo retículo como 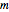 pero es más sencillo.
pero es más sencillo.
In[9]:=
g = r.Inverse[v];
g // MatrixFormOut[9]//MatrixForm=
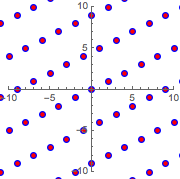
Visualice el retículo generado por las filas de 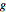 .
.
In[10]:=
ptsg = Flatten[
Table[j First[g] + k Last[g], {j, -12, 12}, {k, -12, 12}], 1];In[11]:=
graphicsg =
Graphics[{Red, PointSize[Medium], Point@ptsg}, PlotRange -> 10,
Axes -> True]Out[11]=
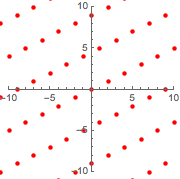
Con la superposición del nuevo retículo sobre el original, se puede ver que son el mismo.
In[12]:=
Show[{graphicsb, graphicsg}]Out[12]=