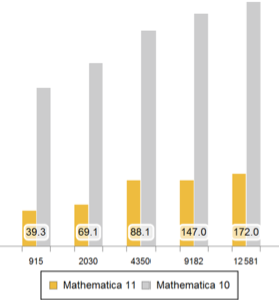
Rotaciones de Euler
La versión 11 introduce EulerMatrix para describir una secuencia de rotaciones con respecto a un marco de coordenadas móvil.
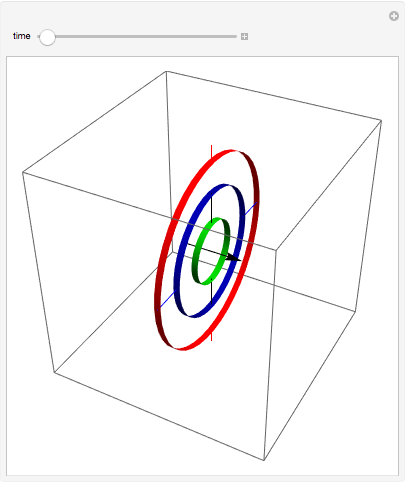
Modele un cardán. Cada ángulo de Euler es el ángulo relativo del giro de cada eje.
muestre la entrada completa de Wolfram Language
In[2]:=

gimbal[{\[Alpha]_, \[Beta]_, \[Gamma]_}] :=
Graphics3D[{GeometricTransformation[ring3,
EulerMatrix[{\[Alpha], 0, 0}]],
GeometricTransformation[ring2,
EulerMatrix[{\[Alpha], \[Beta], 0}]],
GeometricTransformation[ring1,
EulerMatrix[{\[Alpha], \[Beta], \[Gamma]}]]},
ViewPoint -> {1.3, -2.4, 2.}, PlotRange -> 3.5,
ImageSize -> Medium];In[3]:=
gimbalframes = Table[gimbal[{i, i, i}], {i, 0, 2 Pi, Pi/32}];In[4]:=
Manipulate[
gimbalframes[[i]], {{i, 1, "time"}, 1, Length[gimbalframes], 1},
SaveDefinitions -> True]Out[4]=