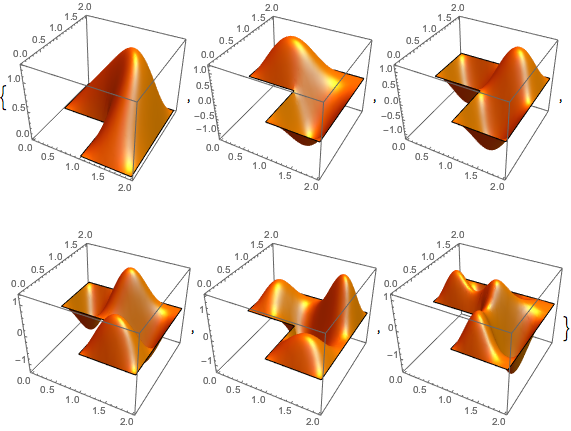
L字形の領域の固有関数を計算する
L字形の領域を指定する.
In[1]:=
L = Polygon[{{1, 0}, {2, 0}, {2, 2}, {0, 2}, {0, 1}, {1, 1}}];ラプラス演算子を指定する.
In[2]:=
\[ScriptCapitalL] = Laplacian[u[x, y], {x, y}];ディリクレ境界条件を指定する.
In[3]:=
\[ScriptCapitalB] = DirichletCondition[u[x, y] == 0., True];L字形の領域で固有関数を計算する.
In[4]:=
{vals, funs} =
NDEigensystem[{\[ScriptCapitalL], \[ScriptCapitalB]},
u[x, y], {x, y} \[Element] L, 6];固有値を調べる.
In[5]:=
valsOut[5]=
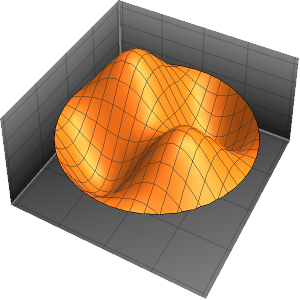
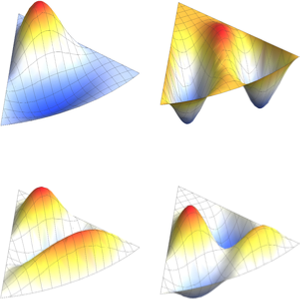
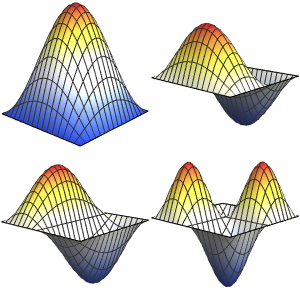
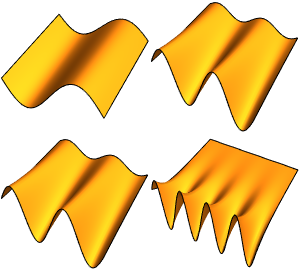
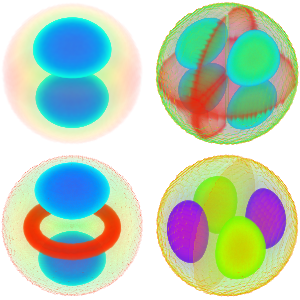
固有関数を可視化する.
In[6]:=

Plot3D[#, {x, y} \[Element] L, PlotPoints -> 75, Mesh -> None,
PlotStyle -> Directive[Orange, Specularity[White, 30]],
BoxRatios -> {1, 1, 0.8}] & /@ funsOut[6]=