Wolfram Language™

Probe the Eigenproblem of a Wave Operator

Find the four smallest eigenvalues and eigenfunctions of a generalized wave equation 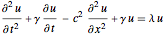over a 1D region.

Set up a generalized wave operator .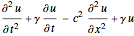

In[1]:=

\[Gamma] = 1.3; c = 1.1; op = D[u[t, x], {t, 2}] + \[Gamma] D[u[t, x], {t, 1}] - c^2 D[u[t, x], {x, 2}] + \[Gamma] u[t, x];

Find the four smallest eigenvalues and eigenfunctions over a 1D region.

In[2]:=

{vals, funs} = NDEigensystem[op == 0, u[t, x], t, {x, 0, \[Pi]}, 4];

Inspect the eigenvalues.

In[3]:=

vals

Out[3]=

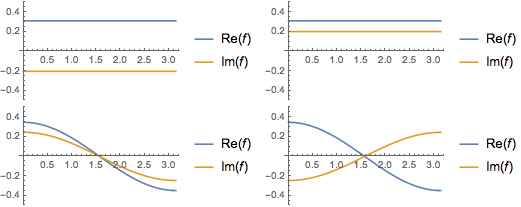
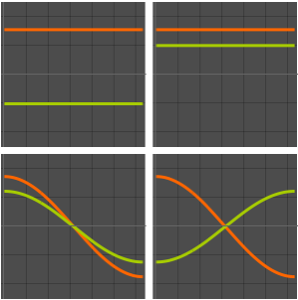
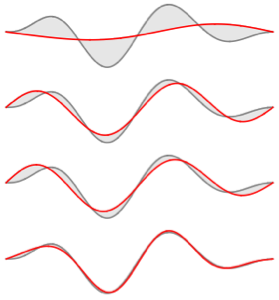
Visualize the real and imaginary parts of the eigenfunctions. Notice the eigenfunctions come in conjugate pairs like the eigenvalues.

In[4]:=

Grid[Partition[ Plot[Evaluate[ReIm[#]], {x, 0, \[Pi]}, PlotRange -> .5, PlotLegends -> {HoldForm@Re[f], HoldForm@Im[f]}] & /@ funs, 2]]

Out[4]=