Find Eigenvalues That Lie in an Interval

Specify a region.

In[1]:=

\[CapitalOmega] = ImplicitRegion[(x^2 + y^2 + 2 y)^2 < 4 (x^2 + y^2), {x, y}];

Specify a Laplacian operator.

In[2]:=

\[ScriptCapitalL] = -Laplacian[u[x, y], {x, y}];

Specify a Dirichlet boundary condition.

In[3]:=

\[ScriptCapitalB] = DirichletCondition[u[x, y] == 0, True];

Find an eigenvalue in a particular interval and the corresponding eigenfunction using a refined mesh.

In[4]:=

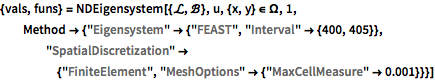
{vals, funs} = NDEigensystem[{\[ScriptCapitalL], \[ScriptCapitalB]}, u, {x, y} \[Element] \[CapitalOmega], 1, Method -> {"Eigensystem" -> {"FEAST", "Interval" -> {400, 405}}, "SpatialDiscretization" -> {"FiniteElement", "MeshOptions" -> {"MaxCellMeasure" -> 0.001}}}]

Out[4]=

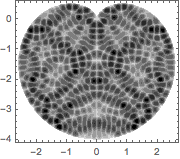
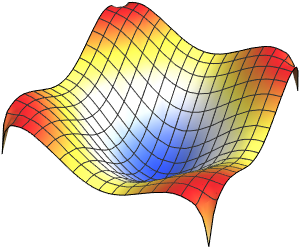
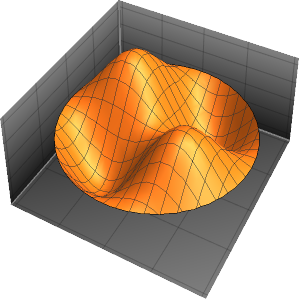
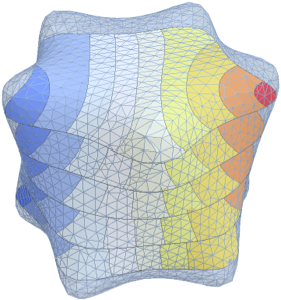
Visualize the eigenfunction found.

In[5]:=

ContourPlot[ Evaluate[Abs[funs[[1]][x, y]]^(1/2)], {x, y} \[Element] funs[[1]]["ElementMesh"], PlotPoints -> 200, ColorFunction -> (GrayLevel[1 - #] &), AspectRatio -> Automatic, ContourStyle -> None, PlotRange -> All, MaxRecursion -> 0]

Out[5]=