Find a 1D Laplacian's Symbolic Eigenfunctions

Specify a 1D Laplacian operator.

In[1]:=

\[ScriptCapitalL] = -Laplacian[u[x], {x}];

Specify homogeneous Dirichlet boundary conditions for the eigenfunctions.

In[2]:=

\[ScriptCapitalB]1 = DirichletCondition[u[x] == 0, True];

Find the five smallest eigenvalues and eigenfunctions.

In[3]:=

{vals, funs} = DEigensystem[{\[ScriptCapitalL], \[ScriptCapitalB]1}, u[x], {x, 0, \[Pi]}, 5];

Inspect the eigenvalues.

In[4]:=

vals

Out[4]=

Inspect the eigenfunctions.

In[5]:=

funs

Out[5]=

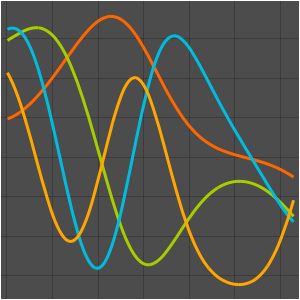
Visualize the eigenfunctions.

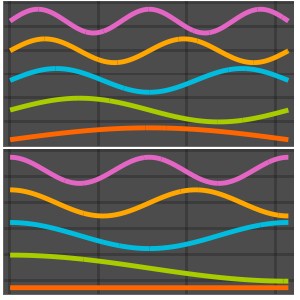
In[6]:=

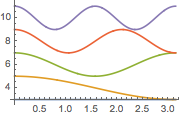
Plot[Evaluate[funs + 2 Range[5]], {x, 0, \[Pi]}]

Out[6]=

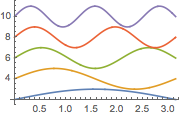
Specify a homogeneous Neumann boundary condition.

In[7]:=

\[ScriptCapitalB]2 = NeumannValue[0, True];

Find the five smallest eigenvalues and eigenfunctions.

In[8]:=

{vals, funs} = DEigensystem[\[ScriptCapitalL] + \[ScriptCapitalB]2, u[x], {x, 0, \[Pi]}, 5];

Inspect the eigenvalues. Relative to the Dirichlet conditions, a zero mode has been added.

In[9]:=

vals

Out[9]=

Sines have replaced cosines in the eigenfunctions.

In[10]:=

funs

Out[10]=

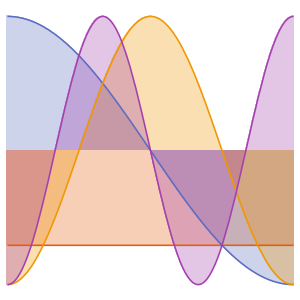
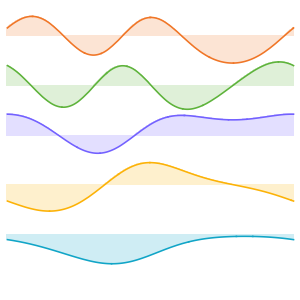
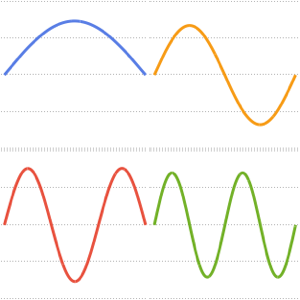
Visualize the eigenfunctions.

In[11]:=

Plot[Evaluate[funs + 2 Range[5]], {x, 0, \[Pi]}]

Out[11]=