多変量の正規性検定

BaringhausHenzeTestは，経験的特性関数に基づく検定統計値で行う多変量の正規性検定である．これは，Baringhaus–Henze–Epps–Pulley (BHEP)検定としても知られている．

In[1]:=

data = RandomVariate[NormalDistribution[], {10^3, 3}];

In[2]:=

BaringhausHenzeTest[data]

Out[2]=

検定統計値は，データのアフィン変換では不変である．

In[3]:=

data2 = AffineTransform[{RandomReal[1, {3, 3}], RandomReal[1, 3]}][ data]; {BaringhausHenzeTest[data2, "TestStatistic"], BaringhausHenzeTest[data, "TestStatistic"]}

Out[3]=

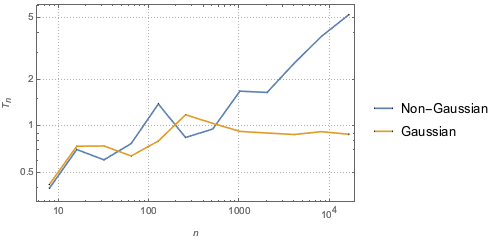
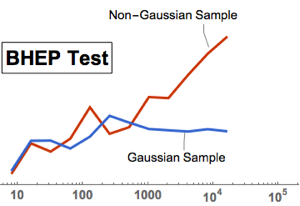
検定統計値は，他のすべての検定に対しても一定である．つまり，データがガウス(Gaussian)分布からのものでない限り，統計値はサンプルサイズが大きくなるにつれて際限なく増える．

In[4]:=

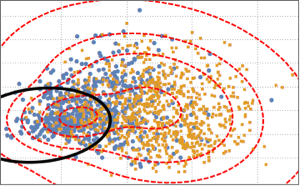
covm = {{2, 1, 0}, {1, 3, -1}, {0, -1, 2}}; ng\[ScriptCapitalD] = MultivariateTDistribution[covm, 12]; g\[ScriptCapitalD] = MultinormalDistribution[{0, 0, 0}, covm];

多変量の 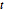分布と多変量の正規分布からサンプルを取る．

In[5]:=

nongaussianData = RandomVariate[ng\[ScriptCapitalD], 2^14]; gaussianData = RandomVariate[g\[ScriptCapitalD], 2^14];

BHEP検定の統計値をサンプルサイズの関数として計算し可視化する．

In[6]:=

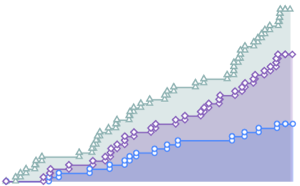
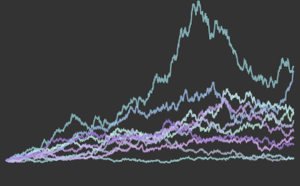
sizes = 2^Range[3, 14]; {nonGaussianTestStatistic, GaussianTestStatistic} = ParallelTable[{size, BaringhausHenzeTest[Take[d, size], "TestStatistic"]}, {d, {nongaussianData, gaussianData}}, {size, sizes}];

In[7]:=

ListLogLogPlot[{nonGaussianTestStatistic, GaussianTestStatistic}, PlotLegends -> {"Non-Gaussian", "Gaussian"}, ImageSize -> Medium, PlotRange -> All, FrameLabel -> {n, Subscript[T, n]}, PlotTheme -> "Detailed", Joined -> True]

Out[7]=