Teste de normalidade multivariado: Novos Recursos do Wolfram Language 11

Teste de normalidade multivariado

BaringhausHenzeTest é um teste de normalidade multivariado com o teste estatístico baseado na função de características empíricas. É conhecido também como o teste de Baringhaus–Henze–Epps–Pulley (BHEP).

In[1]:=

data = RandomVariate[NormalDistribution[], {10^3, 3}];

In[2]:=

BaringhausHenzeTest[data]

Out[2]=

O teste estatístico é invariante sob transformações afins dos dados.

In[3]:=

data2 = AffineTransform[{RandomReal[1, {3, 3}], RandomReal[1, 3]}][
   data];
{BaringhausHenzeTest[data2, "TestStatistic"], 
 BaringhausHenzeTest[data, "TestStatistic"]}

Out[3]=

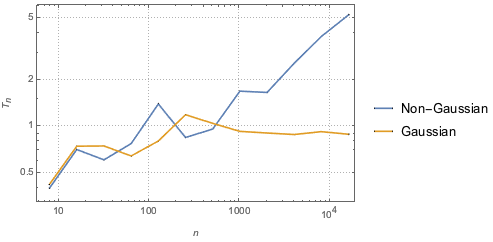
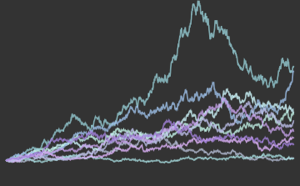
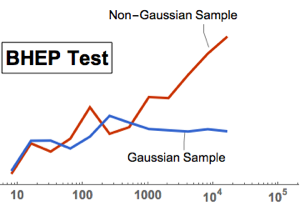
O teste estatístico também é consistente contra cada distribuição alternativa, ou seja, ela cresce sem limites com o tamanho da amostra, a menos que os dados venham de uma distribuição de Gauss.

In[4]:=

covm = {{2, 1, 0}, {1, 3, -1}, {0, -1, 2}};
ng\[ScriptCapitalD] = MultivariateTDistribution[covm, 12];
g\[ScriptCapitalD] = MultinormalDistribution[{0, 0, 0}, covm];

Extraia amostras de uma distribuição t multivariada e de uma distribuição normal multivariada.

In[5]:=

nongaussianData = RandomVariate[ng\[ScriptCapitalD], 2^14];
gaussianData = RandomVariate[g\[ScriptCapitalD], 2^14];

Calcule e visualize o teste estatístico de BHEP como uma função de tamanho de amostra.

In[6]:=

sizes = 2^Range[3, 14];
{nonGaussianTestStatistic, GaussianTestStatistic} = 
  ParallelTable[{size, 
    BaringhausHenzeTest[Take[d, size], 
     "TestStatistic"]}, {d, {nongaussianData, gaussianData}}, {size, 
    sizes}];

mostre o input completo da Wolfram Language

In[7]:=

ListLogLogPlot[{nonGaussianTestStatistic, GaussianTestStatistic}, 
 PlotLegends -> {"Non-Gaussian", "Gaussian"}, ImageSize -> Medium, 
 PlotRange -> All, FrameLabel -> {n, Subscript[T, n]}, 
 PlotTheme -> "Detailed", Joined -> True]

Out[7]=