Wolfram 언어™

다변량의 정규성 검정

BaringhausHenzeTest는 경험적 특성 함수에 기초하여 검정 통계값을 행하는 다변량의 정규성을 검정합니다. 이것은 Baringhaus–Henze–Epps–Pulley (BHEP) 검정으로도 알려져 있습니다.

In[1]:=

data = RandomVariate[NormalDistribution[], {10^3, 3}];

In[2]:=

BaringhausHenzeTest[data]

Out[2]=

검정 통계값은 데이터의 아핀 변환에 불변합니다.

In[3]:=

data2 = AffineTransform[{RandomReal[1, {3, 3}], RandomReal[1, 3]}][ data]; {BaringhausHenzeTest[data2, "TestStatistic"], BaringhausHenzeTest[data, "TestStatistic"]}

Out[3]=

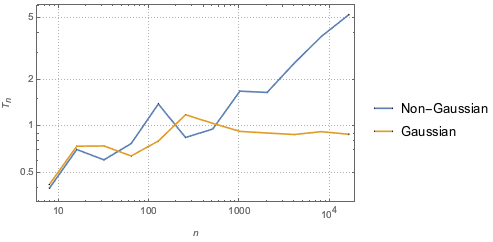
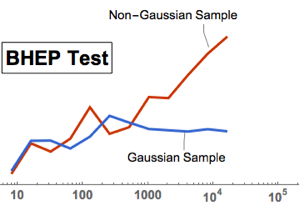
검정 통계 값은 다른 모든 검정에 대해서도 역시 일정합니다. 즉, 데이터가 가우스 분포에서 가져온 것이 아닌 한 통계는 표본 크기가 커질수록 끝없이 늘어납니다.

In[4]:=

covm = {{2, 1, 0}, {1, 3, -1}, {0, -1, 2}}; ng\[ScriptCapitalD] = MultivariateTDistribution[covm, 12]; g\[ScriptCapitalD] = MultinormalDistribution[{0, 0, 0}, covm];

다변량 t 분포 및 다변량 정규 분포에서 샘플을 가져옵니다.

In[5]:=

nongaussianData = RandomVariate[ng\[ScriptCapitalD], 2^14]; gaussianData = RandomVariate[g\[ScriptCapitalD], 2^14];

BHEP 검정 통계 값을 샘플 크기 함수로 계산하고 시각화합니다.

In[6]:=

sizes = 2^Range[3, 14]; {nonGaussianTestStatistic, GaussianTestStatistic} = ParallelTable[{size, BaringhausHenzeTest[Take[d, size], "TestStatistic"]}, {d, {nongaussianData, gaussianData}}, {size, sizes}];

In[7]:=

ListLogLogPlot[{nonGaussianTestStatistic, GaussianTestStatistic}, PlotLegends -> {"Non-Gaussian", "Gaussian"}, ImageSize -> Medium, PlotRange -> All, FrameLabel -> {n, Subscript[T, n]}, PlotTheme -> "Detailed", Joined -> True]

Out[7]=