多元正态性检验

BaringhausHenzeTest 是基于经验特征函数的检验统计的多元正态性检验. 它也被称为 Baringhaus–Henze–Epps–Pulley（BHEP）检验.

In[1]:=

data = RandomVariate[NormalDistribution[], {10^3, 3}];

In[2]:=

BaringhausHenzeTest[data]

Out[2]=

检验统计是数据仿射变换中的不变量.

In[3]:=

data2 = AffineTransform[{RandomReal[1, {3, 3}], RandomReal[1, 3]}][ data]; {BaringhausHenzeTest[data2, "TestStatistic"], BaringhausHenzeTest[data, "TestStatistic"]}

Out[3]=

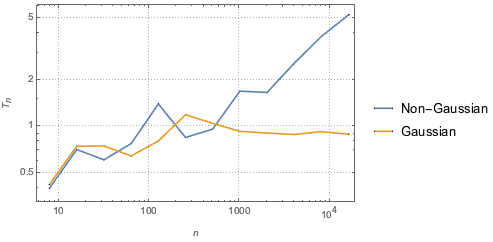
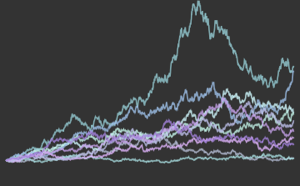
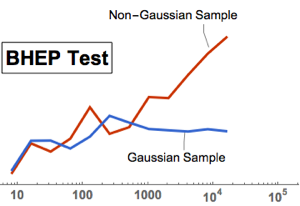
检验统计对于其他每个分布也是一致的. 即，它随样本大小无界增长，除非数据来自高斯分布.

In[4]:=

covm = {{2, 1, 0}, {1, 3, -1}, {0, -1, 2}}; ng\[ScriptCapitalD] = MultivariateTDistribution[covm, 12]; g\[ScriptCapitalD] = MultinormalDistribution[{0, 0, 0}, covm];

从多元 t 分布和多元正态分布抽取样本.

In[5]:=

nongaussianData = RandomVariate[ng\[ScriptCapitalD], 2^14]; gaussianData = RandomVariate[g\[ScriptCapitalD], 2^14];

将 BHEP 检验统计作为样本大小的函数进行计算和可视化.

In[6]:=

sizes = 2^Range[3, 14]; {nonGaussianTestStatistic, GaussianTestStatistic} = ParallelTable[{size, BaringhausHenzeTest[Take[d, size], "TestStatistic"]}, {d, {nongaussianData, gaussianData}}, {size, sizes}];

In[7]:=

ListLogLogPlot[{nonGaussianTestStatistic, GaussianTestStatistic}, PlotLegends -> {"Non-Gaussian", "Gaussian"}, ImageSize -> Medium, PlotRange -> All, FrameLabel -> {n, Subscript[T, n]}, PlotTheme -> "Detailed", Joined -> True]

Out[7]=