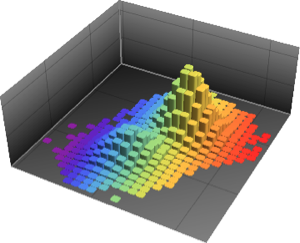
Test de normalité multivariée : Nouveautés de Wolfram Language 11

Test de normalité multivariée

BaringhausHenzeTest est un test de normalité multivariée avec la statistique de test basée sur la fonction caractéristique empirique. Il est également connu sous le nom de test de Baringhaus–Henze–Epps–Pulley (BHEP)

In[1]:=

data = RandomVariate[NormalDistribution[], {10^3, 3}];

In[2]:=

BaringhausHenzeTest[data]

Out[2]=

La statistique de test est invariante sous les transformées affines des données.

In[3]:=

data2 = AffineTransform[{RandomReal[1, {3, 3}], RandomReal[1, 3]}][
   data];
{BaringhausHenzeTest[data2, "TestStatistic"], 
 BaringhausHenzeTest[data, "TestStatistic"]}

Out[3]=

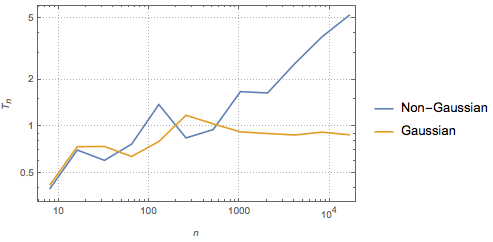
La statistique de test est également cohérente par rapport à toute loi alternative, c'est-à-dire qu'elle croît de manière illimitée avec la taille de l'échantillon, sauf si les données proviennent d'une loi gaussienne.

In[4]:=

covm = {{2, 1, 0}, {1, 3, -1}, {0, -1, 2}};
ng\[ScriptCapitalD] = MultivariateTDistribution[covm, 12];
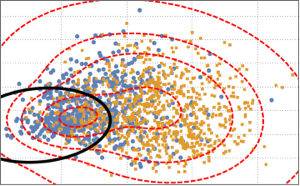
g\[ScriptCapitalD] = MultinormalDistribution[{0, 0, 0}, covm];

Tracez des échantillons d'une loi multivariée t et d'une loi normale multivariée.

In[5]:=

nongaussianData = RandomVariate[ng\[ScriptCapitalD], 2^14];
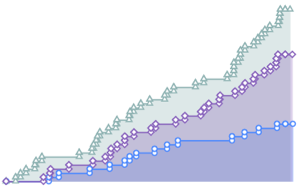
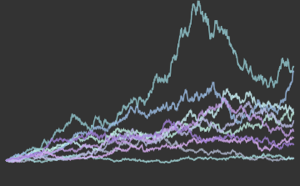
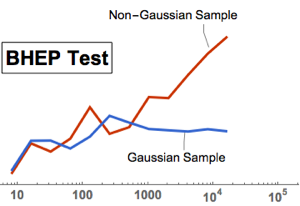
gaussianData = RandomVariate[g\[ScriptCapitalD], 2^14];

Calculez et visualisez les statistiques de test de BHEP en fonction de la taille de l'échantillon.

In[6]:=

sizes = 2^Range[3, 14];
{nonGaussianTestStatistic, GaussianTestStatistic} = 
  ParallelTable[{size, 
    BaringhausHenzeTest[Take[d, size], 
     "TestStatistic"]}, {d, {nongaussianData, gaussianData}}, {size, 
    sizes}];

Afficher l'entrée complète de Wolfram Language

In[7]:=

ListLogLogPlot[{nonGaussianTestStatistic, GaussianTestStatistic}, 
 PlotLegends -> {"Non-Gaussian", "Gaussian"}, ImageSize -> Medium, 
 PlotRange -> All, FrameLabel -> {n, Subscript[T, n]}, 
 PlotTheme -> "Detailed", Joined -> True]

Out[7]=