Многофакторный дисперсионный анализ: Новое в системе Wolfram Language 11

Многофакторный дисперсионный анализ

Тест Барингхаусa-Хенце BaringhausHenzeTest является многомерным тестом дисперсии на основе эмпирической характеристической функции. Он также известен как Baringhaus–Henze–Epps–Pulley (BHEP) тест.

In[1]:=

data = RandomVariate[NormalDistribution[], {10^3, 3}];

In[2]:=

BaringhausHenzeTest[data]

Out[2]=

Тестовая статистика инвариантна относительно аффинных преобразований данных.

In[3]:=

data2 = AffineTransform[{RandomReal[1, {3, 3}], RandomReal[1, 3]}][
   data];
{BaringhausHenzeTest[data2, "TestStatistic"], 
 BaringhausHenzeTest[data, "TestStatistic"]}

Out[3]=

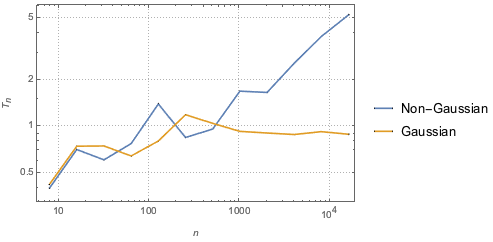
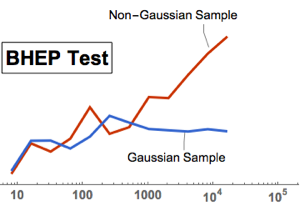
Тестовая статистика также согласуется с любым альтернативным распределением; это означат, что её значение растет согласно размеру выборки, за исключением случаев, когда данные соответствуют параметрам распределения Гаусса.

In[4]:=

covm = {{2, 1, 0}, {1, 3, -1}, {0, -1, 2}};
ng\[ScriptCapitalD] = MultivariateTDistribution[covm, 12];
g\[ScriptCapitalD] = MultinormalDistribution[{0, 0, 0}, covm];

Построим выборки на основе многомерного t-распределения и многомерного нормального распределения.

In[5]:=

nongaussianData = RandomVariate[ng\[ScriptCapitalD], 2^14];
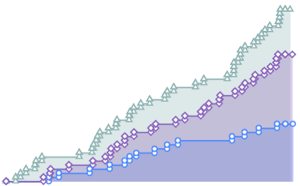
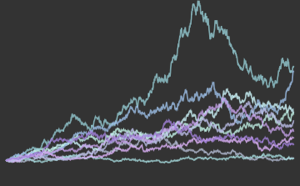
gaussianData = RandomVariate[g\[ScriptCapitalD], 2^14];

Вычислим и визуализируем результат теста Барингхауса-Хенце (BHEP) для выборок разной величины.

In[6]:=

sizes = 2^Range[3, 14];
{nonGaussianTestStatistic, GaussianTestStatistic} = 
  ParallelTable[{size, 
    BaringhausHenzeTest[Take[d, size], 
     "TestStatistic"]}, {d, {nongaussianData, gaussianData}}, {size, 
    sizes}];

код на языке Wolfram Language целиком

In[7]:=

ListLogLogPlot[{nonGaussianTestStatistic, GaussianTestStatistic}, 
 PlotLegends -> {"Non-Gaussian", "Gaussian"}, ImageSize -> Medium, 
 PlotRange -> All, FrameLabel -> {n, Subscript[T, n]}, 
 PlotTheme -> "Detailed", Joined -> True]

Out[7]=