Prueba multivariable de normalidad: Nuevo en Wolfram Language 11

Prueba multivariable de normalidad

BaringhausHenzeTest es una prueba multivariable de normalidad con la prueba estadística basada en la función de características empíricas. También se le conoce como la prueba de Baringhaus–Henze–Epps–Pulley (BHEP).

In[1]:=

data = RandomVariate[NormalDistribution[], {10^3, 3}];

In[2]:=

BaringhausHenzeTest[data]

Out[2]=

La prueba estadística es invariante bajo transformaciones afines de los datos.

In[3]:=

data2 = AffineTransform[{RandomReal[1, {3, 3}], RandomReal[1, 3]}][
   data];
{BaringhausHenzeTest[data2, "TestStatistic"], 
 BaringhausHenzeTest[data, "TestStatistic"]}

Out[3]=

La prueba estadística también es consistente bajo cada distribución alternativa; es decir, esta crece ilimitadamente con el tamaño de muestra a menos que provenga de una distribución gaussiana.

In[4]:=

covm = {{2, 1, 0}, {1, 3, -1}, {0, -1, 2}};
ng\[ScriptCapitalD] = MultivariateTDistribution[covm, 12];
g\[ScriptCapitalD] = MultinormalDistribution[{0, 0, 0}, covm];

Extraiga muestras de una distribución t multivariable y de una distribución normal multivariable.

In[5]:=

nongaussianData = RandomVariate[ng\[ScriptCapitalD], 2^14];
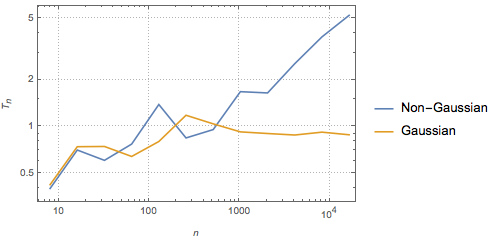
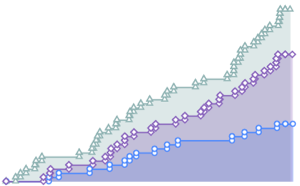
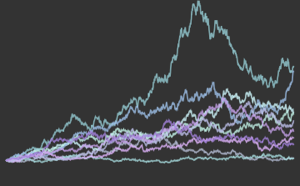
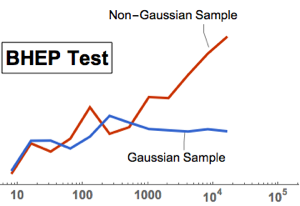
gaussianData = RandomVariate[g\[ScriptCapitalD], 2^14];

Calcule y visualice la prueba estadística de BHEP como una función de tamaño de muestra.

In[6]:=

sizes = 2^Range[3, 14];
{nonGaussianTestStatistic, GaussianTestStatistic} = 
  ParallelTable[{size, 
    BaringhausHenzeTest[Take[d, size], 
     "TestStatistic"]}, {d, {nongaussianData, gaussianData}}, {size, 
    sizes}];

muestre la entrada completa de Wolfram Language

In[7]:=

ListLogLogPlot[{nonGaussianTestStatistic, GaussianTestStatistic}, 
 PlotLegends -> {"Non-Gaussian", "Gaussian"}, ImageSize -> Medium, 
 PlotRange -> All, FrameLabel -> {n, Subscript[T, n]}, 
 PlotTheme -> "Detailed", Joined -> True]

Out[7]=