Mercator sphérique ou ellipsoïdal

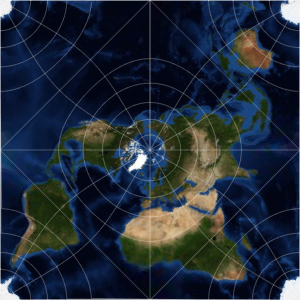
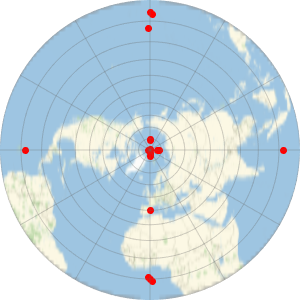
La projection de Mercator produit des résultats différents avec un modèle sphérique de la Terre et un modèle ellipsoïdal de la Terre. Wolfram Language vous permet de travailler avec les deux cas.

La projection utilisée dans la plupart des serveurs Web de carte utilise un modèle sphérique de la Terre, et il est généralement appelé « web Mercator ».

In[1]:=

webMercator = {"Mercator", "ReferenceModel" -> GeodesyData["WGS84", "SemimajorAxis"]}

Out[1]=

In[2]:=

ellipMercator = {"Mercator", "ReferenceModel" -> "WGS84"}

Out[2]=

Transformez l'emplacement de l'université d'Oxford en utilisant les deux projections.

In[3]:=

p = GeoPosition[ Entity["University", "UniversityOfOxfordUnitedKingdom36022"]]

Out[3]=

In[4]:=

GeoGridPosition[p, webMercator][[1]]

Out[4]=

In[5]:=

GeoGridPosition[p, ellipMercator][[1]]

Out[5]=

Il y a une différence correspondant à plus de 33 kilomètres dans la coordonnée nord.

In[6]:=

GeoGridPosition[p, webMercator][[1]]; GeoGridPosition[p, ellipMercator][[1]]; %% - %

Out[6]=

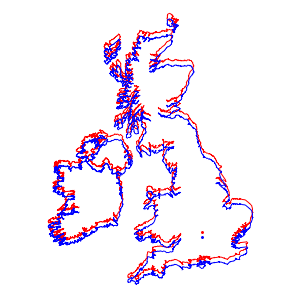
En utilisant les deux projections, dessinez les cartes respectives du Royaume-Uni et de l'Irlande, qui sont pratiquement identiques.

In[7]:=

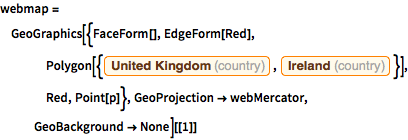
webmap = GeoGraphics[{FaceForm[], EdgeForm[Red], Polygon[{Entity["Country", "UnitedKingdom"], Entity["Country", "Ireland"]}], Red, Point[p]}, GeoProjection -> webMercator, GeoBackground -> None][[1]]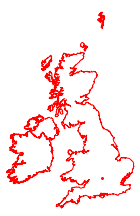

Out[7]=

In[8]:=

ellipmap = GeoGraphics[{FaceForm[], EdgeForm[Blue], Polygon[{Entity["Country", "UnitedKingdom"], Entity["Country", "Ireland"]}], Blue, Point[p]}, GeoProjection -> ellipMercator, GeoBackground -> None][[1]]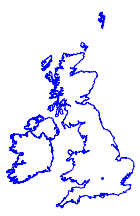

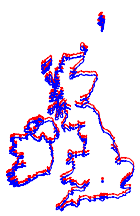
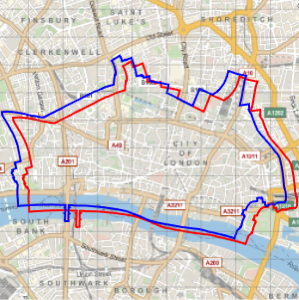
Out[8]=

Toutefois, lorsqu'elles sont superposées sur la même carte, nous pouvons clairement voir la différence.

In[9]:=

Show[webmap, ellipmap]

Out[9]=