Explore a Detailed Model of the Earth's Oceans
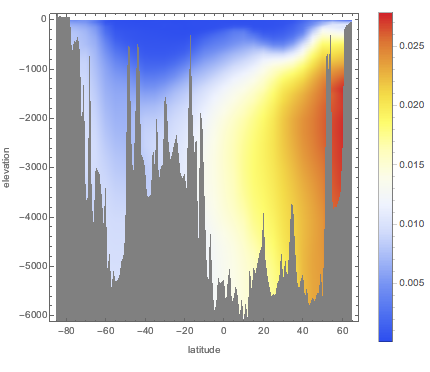
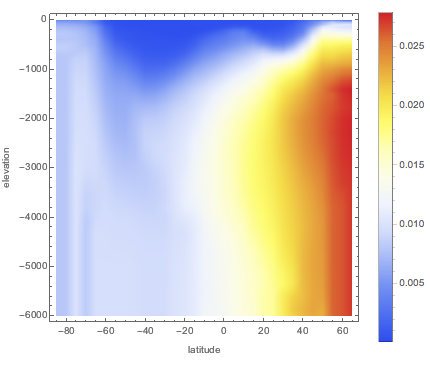
Discover how salinity of seawater deviates at different depths from its standard average value of 35.2 g/kg.
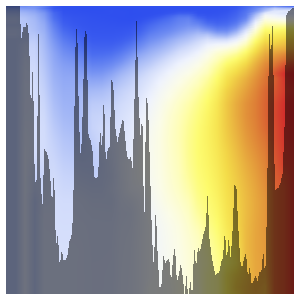
Compute an array of values of salinity anomaly along the 180° E meridian for depths ranging from 0 to 6000 meters, and assuming a constant temperature of 15 °C.
In[1]:=

anomaly =
Table[{lat, Quantity[-d, "Meters"],
StandardOceanData[<|"Position" -> GeoPosition[{lat, 180}],
"Pressure" -> Quantity[d, "Decibars"],
"Temperature" -> Quantity[15, "DegreesCelsius"]|>,
"AbsoluteSalinityAnomaly"]},
{lat, -85, 65, 5}, {d, 0, 6000, 50}];The highest deviations are found for larger latitudes.
In[2]:=

anomalyPlot =
ListDensityPlot[Flatten[anomaly, 1],
ColorFunction -> "TemperatureMap",
FrameLabel -> {"latitude", "elevation"}, PlotLegends -> Automatic,
ImageSize -> Medium]Out[2]=
Superimpose an elevation profile of the sea floor along the same meridian.
show complete Wolfram Language input
Out[3]=