Wolfram Language™

Modélisez la composition de l'univers dans le temps

Explorez la manière dont la composition de l'univers évolue au fil du temps, selon le modèle standard ΛCDM (matière noire froide Lambda).

Calculez les valeurs des rapports de densité de l'énergie noire, de la matière et du rayonnement à différents âges de l'univers, allant de 1000 ans à 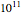ns.

In[1]:=

ages = Quantity[10^Range[3, 11, 0.2], "Years"];

In[2]:=

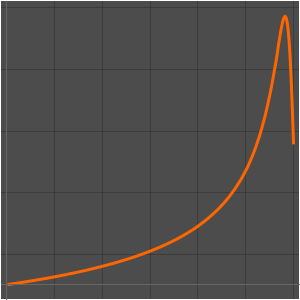
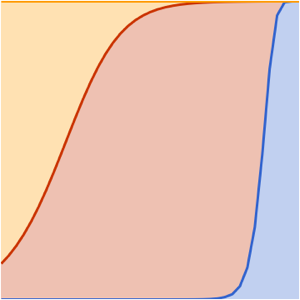
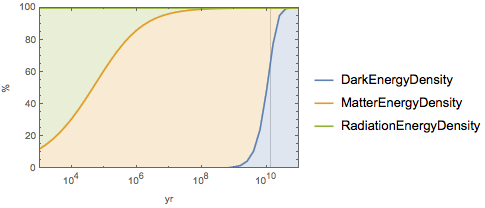
darkenergy = Table[UniverseModelData[t, "DarkEnergyDensityRatio"], {t, ages}]; matter = Table[ UniverseModelData[t, "MatterEnergyDensityRatio"], {t, ages}]; radiation = Table[UniverseModelData[t, "RadiationEnergyDensityRatio"], {t, ages}];

Représentez l'évolution dans le temps pour les trois composantes, indiquant l'âge actuel de l'univers avec une barre verticale. Actuellement, la composante la plus importante est l'énergie noire.

In[3]:=

data = { Transpose[{ages, darkenergy}], Transpose[{ages, darkenergy + matter}], Transpose[{ages, darkenergy + matter + radiation}] }; ListLogLinearPlot[data, PlotRange -> All, Joined -> True, Filling -> {1 -> Axis, 2 -> {1}, 3 -> {2}}, FrameLabel -> Automatic, GridLines -> {{13.8*10^9}, None}, PlotRangePadding -> 0, Frame -> True, PlotLegends -> {"DarkEnergyDensity", "MatterEnergyDensity", "RadiationEnergyDensity"}]

Out[3]=

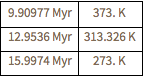
Découvrez à quel moment la température du rayonnement de fond aurait été comprise entre 273 et 373 K (l'« époque habitable » de l'univers).

In[4]:=

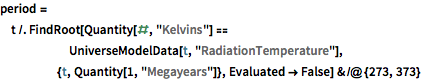
period = t /. FindRoot[ Quantity[#, "Kelvins"] == UniverseModelData[t, "RadiationTemperature"], {t, Quantity[1, "Megayears"]}, Evaluated -> False] & /@ {273, 373}

Out[4]=

In[5]:=

Grid[{#, UniverseModelData[#, "RadiationTemperature"]} & /@ Through[{Min, Mean, Max}[period]], Dividers -> All]

Out[5]=