円形膜の振動を生成する: Wolfram言語 11の新機能

‹›

円形膜の振動を生成する

二次元の波動方程式を使って，半径1の円形膜の振動をモデル化する．

In[1]:=

eqn = r D[u[r, t], {t, 2}] == D[r D[u[r, t], r], r];

膜の境界が固定されたままであるように指定する．

In[2]:=

bc = u[1, t] == 0;

問題の初期条件．

In[3]:=

ic = {u[r, 0] == 0, Derivative[0, 1][u][r, 0] == 1};

DSolveを使って，ベッセル(Bessel)関数についての解を得る．

In[4]:=

(dsol = DSolve[{eqn, bc, ic}, u[r, t], {r, t}]) // TraditionalForm

Out[4]//TraditionalForm=

Inactiveの和から有限数の項を取り出す．

In[5]:=

h[r_, t_] = 
  u[r, t] /. dsol[[1]] /. {\[Infinity] -> 3} // Activate // N;

最低のモードはおよそ2.612の周期を持つ．

In[6]:=

N[(2 \[Pi])/BesselJZero[0, 1]]

Out[6]=

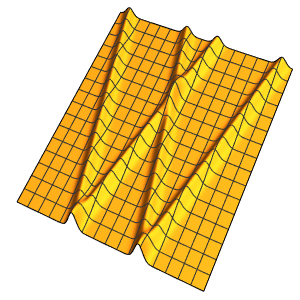
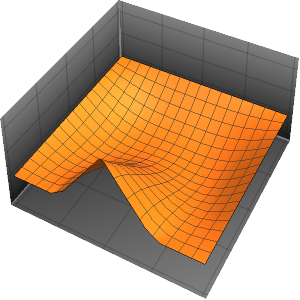
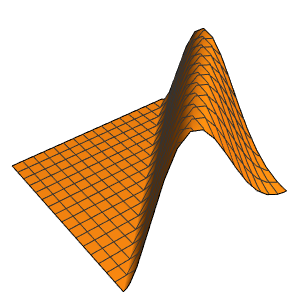
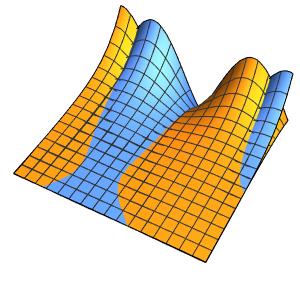
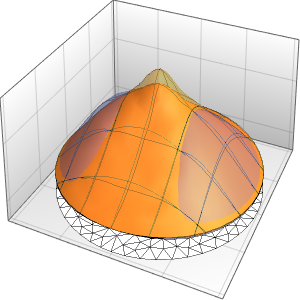
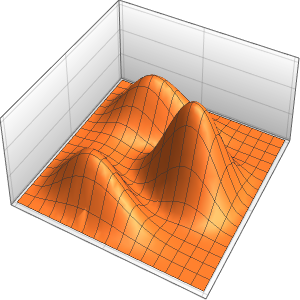
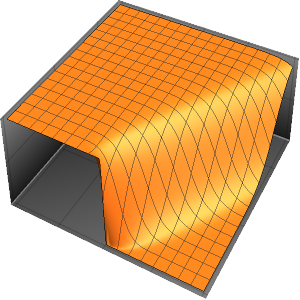
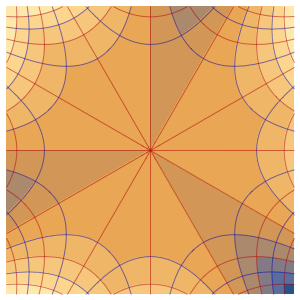
4周期に渡る膜の振動を可視化する．

In[7]:=

ListAnimate[
 Table[Plot3D[
   Evaluate[h[r, t] /. {r -> Sqrt[x^2 + y^2]}], {x, y} \[Element] 
    Disk[], PlotRange -> {-1, 1}, Ticks -> None, Mesh -> True, 
   MeshStyle -> {Red, Blue}, PlotStyle -> Yellow, Boxed -> False, 
   Axes -> False, ImageSize -> Medium, AspectRatio -> 1, 
   Background -> Lighter[Orange, 0.85]], {t, 0, 10.45, 0.05}]]