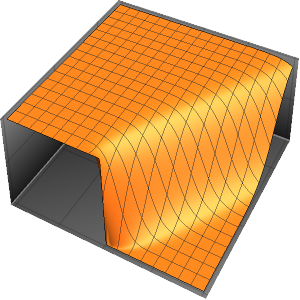
Model the Flow of Heat in an Insulated Bar
Model the flow of heat in a bar of length 1 that is insulated at both ends.
In[1]:=
heqn = D[u[x, t], t] == D[u[x, t], {x, 2}];Specify that no heat flows through the ends of the bar.
In[2]:=
bc = {Derivative[1, 0][u][0, t] == 0, Derivative[1, 0][u][1, t] == 0};Specify an initial condition.
In[3]:=
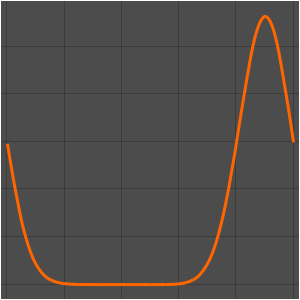
ic = u[x, 0] == 20 + 80 x;Solve the heat equation subject to these conditions.
In[4]:=
sol = DSolve[{heqn, bc, ic}, u[x, t], {x, t}]Out[4]=
Extract a few terms from the Inactive sum.
In[5]:=
approxsol =
u[x, t] /. sol[[1]] /. {Infinity -> 4} // Activate // ExpandOut[5]=
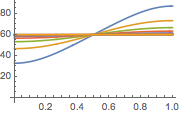
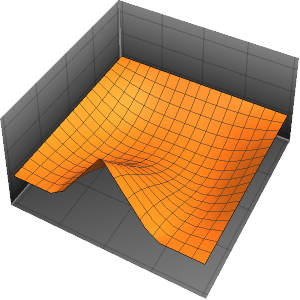
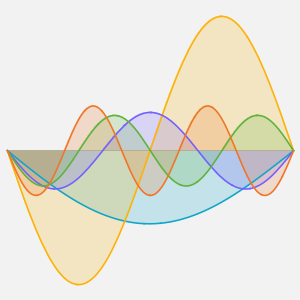
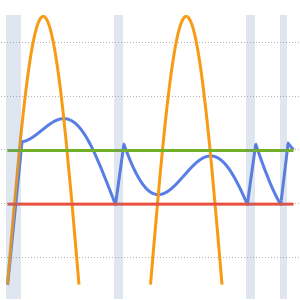
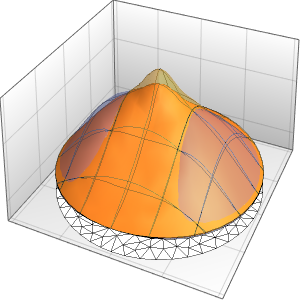
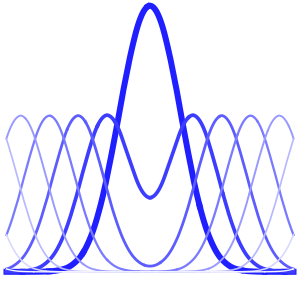
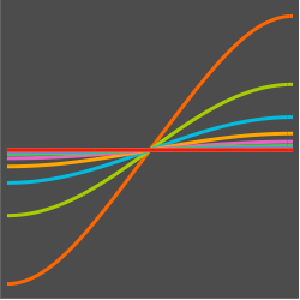
Visualize the evolution of the temperature to the steady-state value of 60°.
In[6]:=
Plot[Table[approxsol, {t, 0.02, 0.9, 0.07}] // Evaluate, {x, 0, 1},
AxesOrigin -> {0, 0}, PlotRange -> All]Out[6]=