Modellieren Sie den Wärmefluss in einem isolierten Balken
Modellieren Sie den Wärmefluss in einem Balken der Länge 1, der an beiden Enden isoliert ist.
In[1]:=
heqn = D[u[x, t], t] == D[u[x, t], {x, 2}];Spezifizieren Sie, dass durch die Enden des Balkens keine Wärme strömt.
In[2]:=
bc = {Derivative[1, 0][u][0, t] == 0, Derivative[1, 0][u][1, t] == 0};Spezifizieren Sie eine Anfangsbedingung.
In[3]:=
ic = u[x, 0] == 20 + 80 x;Lösen Sie die Wärmegleichung unter diesen Bedingungen.
In[4]:=
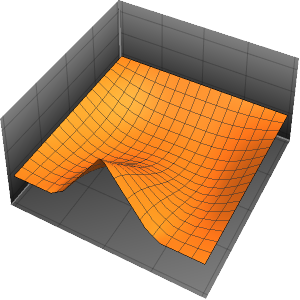
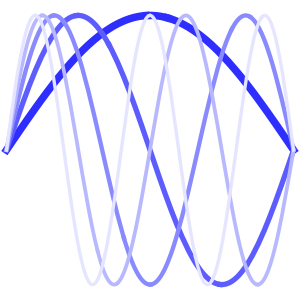
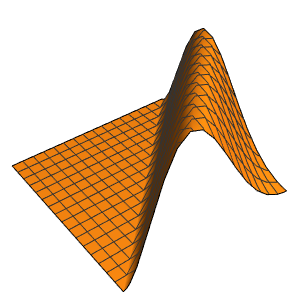
sol = DSolve[{heqn, bc, ic}, u[x, t], {x, t}]Out[4]=
Extrahieren Sie die Terme aus der Inactive-Summe.
In[5]:=
approxsol =
u[x, t] /. sol[[1]] /. {Infinity -> 4} // Activate // ExpandOut[5]=
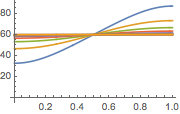
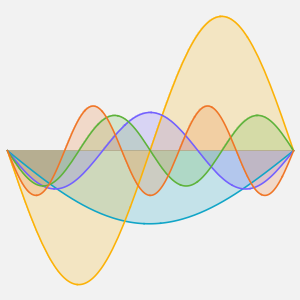
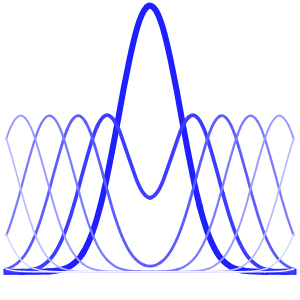
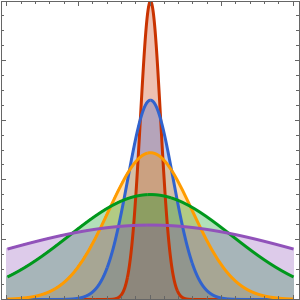
Visualisieren Sie den Temperaturverlauf bis hin zum stationären Zustand von 60°.
In[6]:=
Plot[Table[approxsol, {t, 0.02, 0.9, 0.07}] // Evaluate, {x, 0, 1},
AxesOrigin -> {0, 0}, PlotRange -> All]Out[6]=