Modélisez le flux de chaleur dans une barre isolée

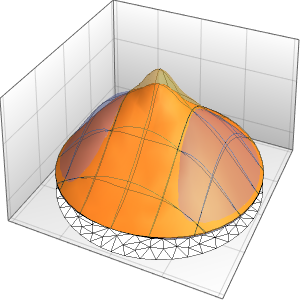
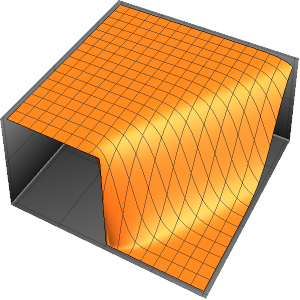
Modélisez le flux de chaleur dans une barre de longueur 1 isolée aux deux extrémités.

In[1]:=

heqn = D[u[x, t], t] == D[u[x, t], {x, 2}];

Indiquez qu'il n'y a aucune chaleur à travers les extrémités de la barre.

In[2]:=

bc = {Derivative[1, 0][u][0, t] == 0, Derivative[1, 0][u][1, t] == 0};

Spécifiez une condition initiale.

In[3]:=

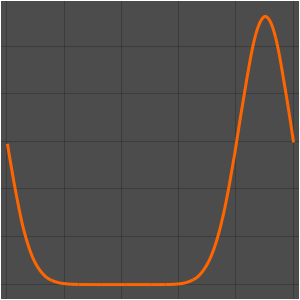
ic = u[x, 0] == 20 + 80 x;

Résolvez l'équation de chaleur sous ces conditions.

In[4]:=

sol = DSolve[{heqn, bc, ic}, u[x, t], {x, t}]

Out[4]=

Extrayez quelques termes de la somme Inactive.

In[5]:=

approxsol = u[x, t] /. sol[[1]] /. {Infinity -> 4} // Activate // Expand

Out[5]=

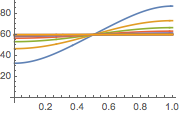
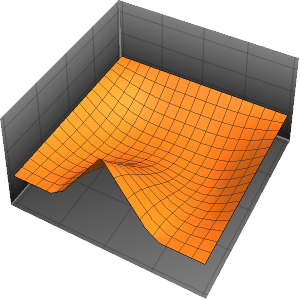
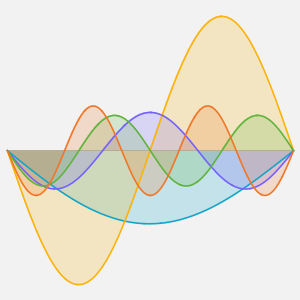
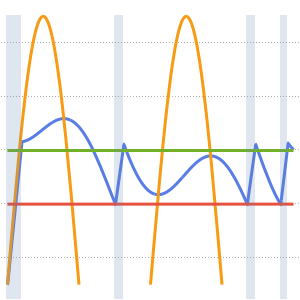
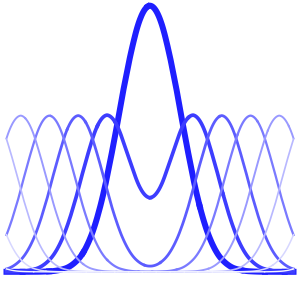
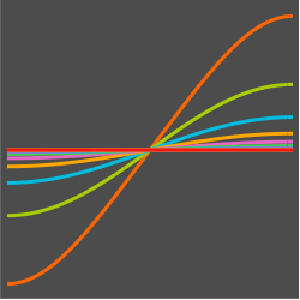
Visualisez l'évolution de la température jusqu'à la valeur stable de 60°.

In[6]:=

Plot[Table[approxsol, {t, 0.02, 0.9, 0.07}] // Evaluate, {x, 0, 1}, AxesOrigin -> {0, 0}, PlotRange -> All]

Out[6]=