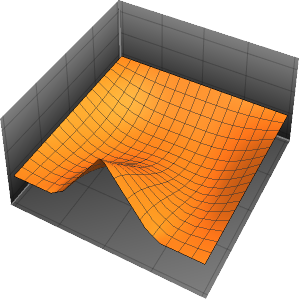
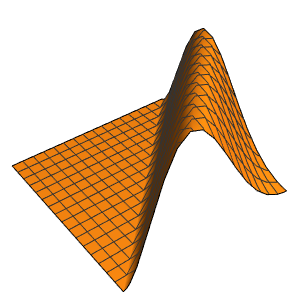
为隔热的棒里的热量流动建立模型
为一个两端都绝热且长度为1的棒的热量流动建立模型.
In[1]:=
heqn = D[u[x, t], t] == D[u[x, t], {x, 2}];假定棒的两端没有热量流过.
In[2]:=
bc = {Derivative[1, 0][u][0, t] == 0, Derivative[1, 0][u][1, t] == 0};指定初始条件.
In[3]:=
ic = u[x, 0] == 20 + 80 x;求解服从这些条件的热传导方程.
In[4]:=
sol = DSolve[{heqn, bc, ic}, u[x, t], {x, t}]Out[4]=
从 Inactive 总和中提取出一些项.
In[5]:=
approxsol =
u[x, t] /. sol[[1]] /. {Infinity -> 4} // Activate // ExpandOut[5]=
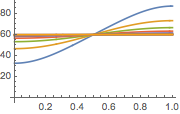
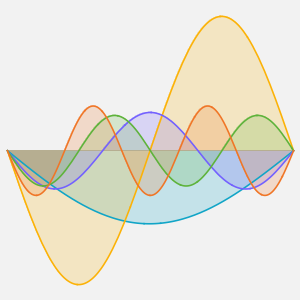
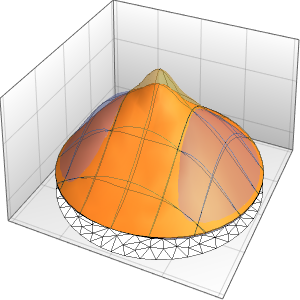
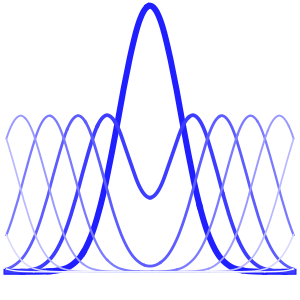
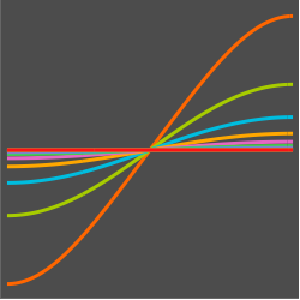
可视化温度向 60°恒定状态值演变的过程.
In[6]:=
Plot[Table[approxsol, {t, 0.02, 0.9, 0.07}] // Evaluate, {x, 0, 1},
AxesOrigin -> {0, 0}, PlotRange -> All]Out[6]=