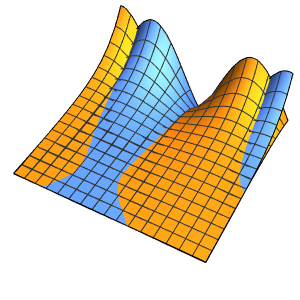
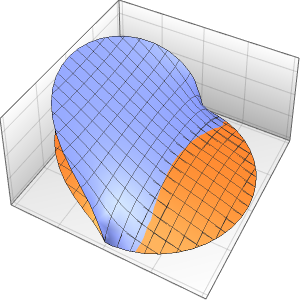
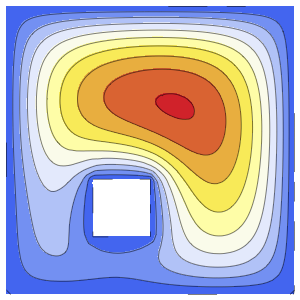
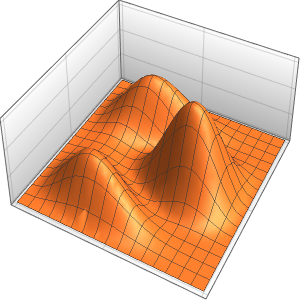
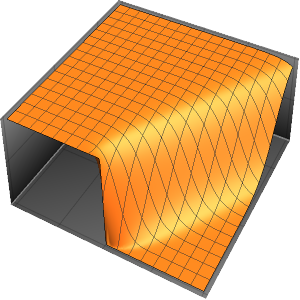
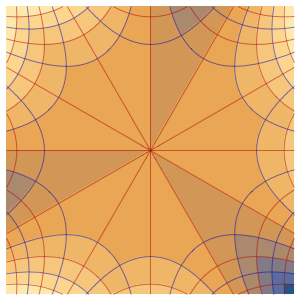
Modele o fluxo de calor em uma barra de isolamento

Modele o fluxo de calor em uma barra de comprimento 1 que esteja isolada em ambos extremos.

In[1]:=

heqn = D[u[x, t], t] == D[u[x, t], {x, 2}];

Especifique que nenhum calor flua através dos extremos da barra.

In[2]:=

bc = {Derivative[1, 0][u][0, t] == 0, Derivative[1, 0][u][1, t] == 0};

Especifique uma codição inicial.

In[3]:=

ic = u[x, 0] == 20 + 80 x;

Resolva a equação de calor sujeita a estas condições.

In[4]:=

sol = DSolve[{heqn, bc, ic}, u[x, t], {x, t}]

Out[4]=

Extraia alguns termos da soma de Inactive.

In[5]:=

approxsol = u[x, t] /. sol[[1]] /. {Infinity -> 4} // Activate // Expand

Out[5]=

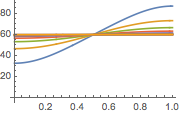
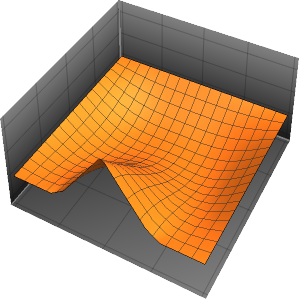
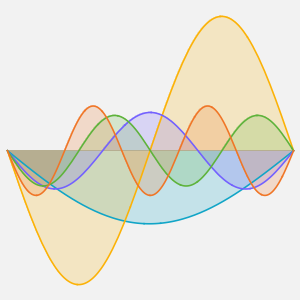
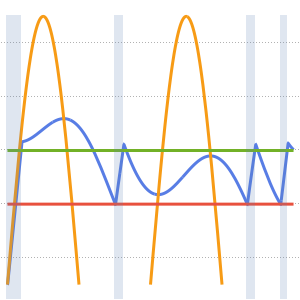
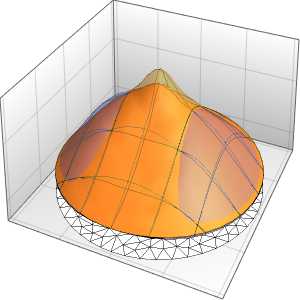
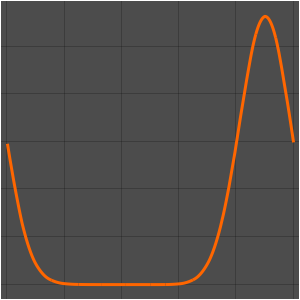
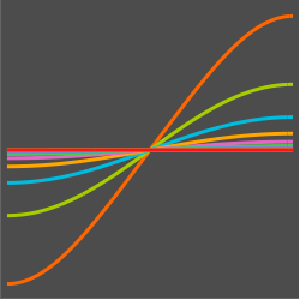
Visualize a evolução da temperatura em um valor estável de 60°.

In[6]:=

Plot[Table[approxsol, {t, 0.02, 0.9, 0.07}] // Evaluate, {x, 0, 1}, AxesOrigin -> {0, 0}, PlotRange -> All]

Out[6]=