断熱された棒の中の熱の流れをモデル化する
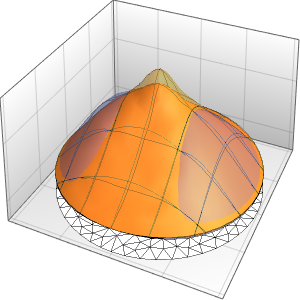
両端が断熱されている長さ1の棒内の熱の流れをモデル化する.
In[1]:=
heqn = D[u[x, t], t] == D[u[x, t], {x, 2}];棒の両端からは熱の流れがないことを指定する.
In[2]:=
bc = {Derivative[1, 0][u][0, t] == 0, Derivative[1, 0][u][1, t] == 0};初期条件を指定する.
In[3]:=
ic = u[x, 0] == 20 + 80 x;これらの条件における熱伝導方程式を解く.
In[4]:=
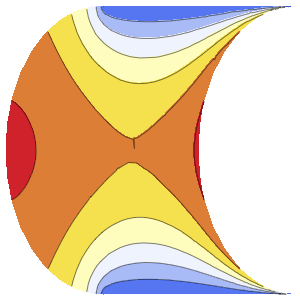
sol = DSolve[{heqn, bc, ic}, u[x, t], {x, t}]Out[4]=
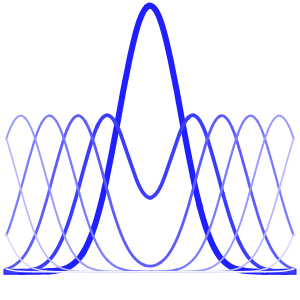
Inactiveの和から数項を取り出す.
In[5]:=
approxsol =
u[x, t] /. sol[[1]] /. {Infinity -> 4} // Activate // ExpandOut[5]=
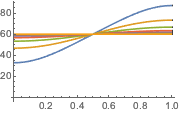
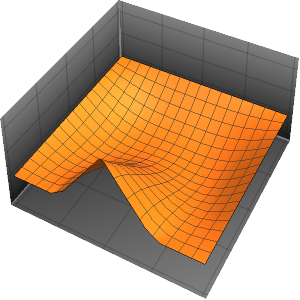
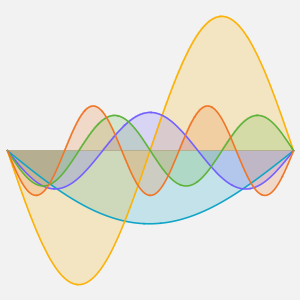
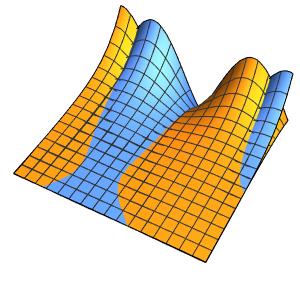
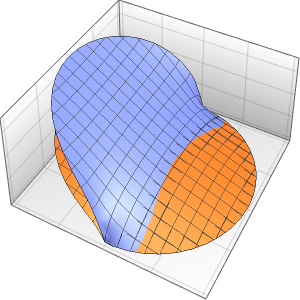
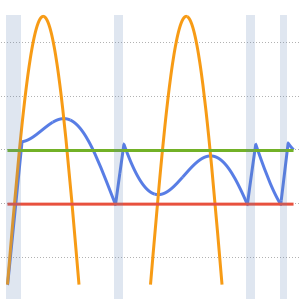
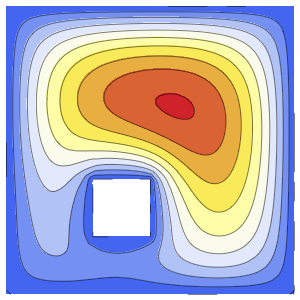
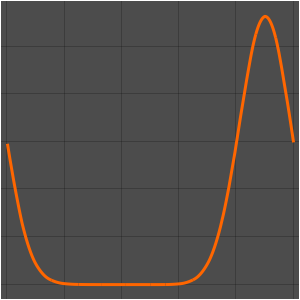
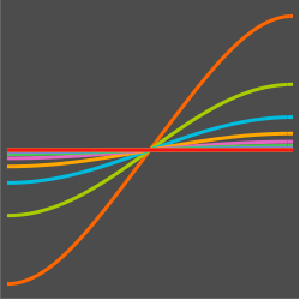
温度が60°の定常状態になるまでの進化を可視化する.
In[6]:=
Plot[Table[approxsol, {t, 0.02, 0.9, 0.07}] // Evaluate, {x, 0, 1},
AxesOrigin -> {0, 0}, PlotRange -> All]Out[6]=