Untersuchen Sie ein Quantenteilchen in einem Kasten: Neu in Wolfram Language 11

Untersuchen Sie ein Quantenteilchen in einem Kasten

Ein frei bewegliches Quantenteilchen in einem zweidimensionalen Rechteck mit den Seiten xMax und yMax ist beschrieben durch die zweidimensionale zeitabhängige Schrödingergleichung, gemeinsam mit den Randbedingungen, die der Wellenfunktion am Rand den Wert von 0 vorschreiben.

In[1]:=

eqn = I D[\[Psi][x, y, t], t] == -\[HBar]^2/(2 m)
     Laplacian[\[Psi][x, y, t], {x, y}];

In[2]:=

bcs = {\[Psi][0, y, t] == 0, \[Psi][xMax, y, t] == 
    0, \[Psi][x, yMax, t] == 0, \[Psi][x, 0, t] == 0};

Diese Gleichung hat eine allgemeine Lösung, die eine formale unendliche Summe sogenannter Eigenzustände ist.

In[3]:=

DSolveValue[{eqn, bcs}, \[Psi][x, y, t], {x, y, t}]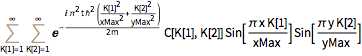

Out[3]=

Definieren Sie eine Anfangsbedingung, die einem Einheits-Eigenzustand gleicht.

In[4]:=

initEigen = \[Psi][x, y, 0] == 
   2 /Sqrt[xMax yMax] Sin[(\[Pi] x)/xMax] Sin[(\[Pi] y)/yMax];

In diesem Fall ist die Lösung einfach ein zeitabhängiges Vielfaches (des Einheitsbetrags) der Anfangsbedingung.

In[5]:=

DSolveValue[{eqn, bcs, initEigen}, \[Psi][x, y, t], {x, y, t}]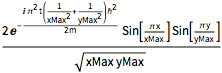

Out[5]=

Definieren Sie eine Anfangsbedingung, die eine Summe von Eigenzuständen ist. Da es sich bei den Anfangsbedingungen nicht um einen Eigenzustand handelt, ist die Aufenthaltswahrscheinlichkeit des Teilchens zeitabhängig.

In[6]:=

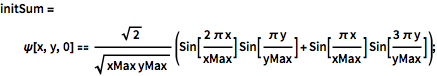
initSum = \[Psi][x, y, 0] == 
   Sqrt[2]/Sqrt[
    xMax yMax] (Sin[(2 \[Pi] x)/xMax] Sin[(\[Pi] y)/yMax] + 
      Sin[(\[Pi] x)/xMax] Sin[(3 \[Pi] y)/yMax]);

Lösen Sie mit der neuen Anfangsbedingung.

In[7]:=

sol = DSolveValue[{eqn, bcs, initSum}, \[Psi][x, y, t], {x, y, t}]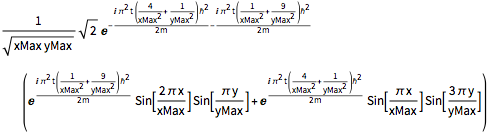

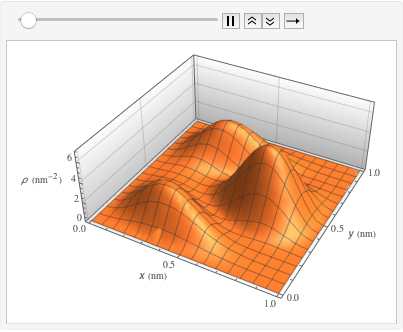
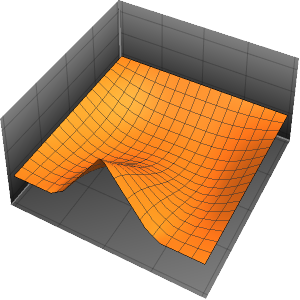
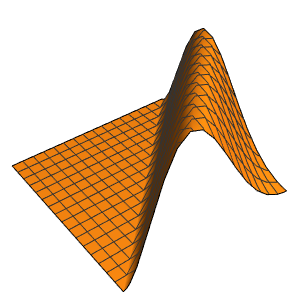
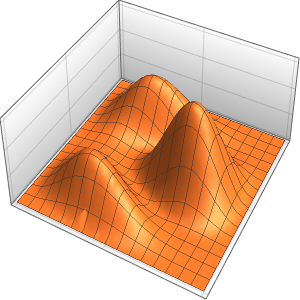
Out[7]=

Berechnen Sie die Wahrscheinlichkeitsdichte, indem Sie die Werte der vereinfachten Planck-Konstante, Elektronenmasse und eines Kastens atomarer Dimensionen unter Verwendung der Einheiten der Elektronenmasse, Nanometer und Femtosekunden, einsetzen.

In[8]:=

\[HBar] = 
 QuantityMagnitude[Quantity[1., "ReducedPlanckConstant"], 
  "ElectronMass" * ("Nanometers")^2/"Femtoseconds"]

Out[8]=

In[9]:=

\[Rho][x_, y_, t_] = 
 FullSimplify[ComplexExpand[Conjugate[sol] sol]] /. {m -> 1, 
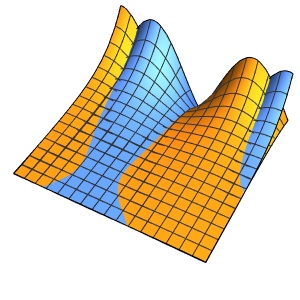
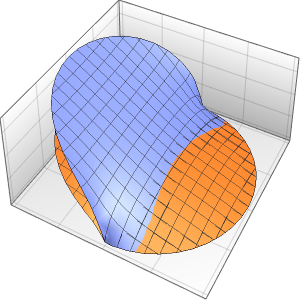
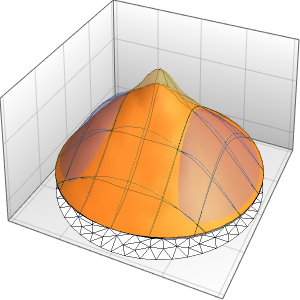
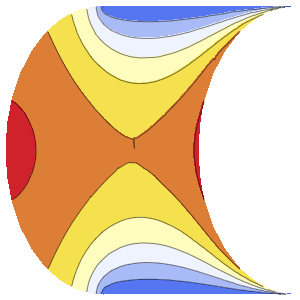
   xMax -> 1, yMax -> 1}

Out[9]=

Visualisieren Sie Wahrscheinlichkeitsdichte innerhalb des Kastens im Laufe der Zeit.

In[10]:=

ListAnimate[
 Table[Plot3D[\[Rho][x , y , t], {x, 0, 1}, {y, 0, 1}, 
   PlotTheme -> {"Scientific", "SolidGrid"}, AxesLabel -> {"\!\(\*
StyleBox[\"x\", \"SO\"]\) (nm)", " \!\(\*
StyleBox[\"y\", \"SO\"]\) (nm)", "\!\(\*
StyleBox[\"\[Rho]\", \"SO\"]\) (\!\(\*SuperscriptBox[\(nm\), \
\(-2\)]\))"}, ImageSize -> Medium, PlotRange -> {0, 7}], {t, 0, 
   19, .5}]]