Wolfram Language™

Untersuchen Sie die Vibrationen einer gespannten Seite

Untersuchen Sie die Vibrationen eine gespannten Saite mithilfe der Wellengleichung.

In[1]:=

weqn = D[u[x, t], {t, 2}] == D[u[x, t], {x, 2}];

Spezifizieren Sie, dass die Enden der Saite während der Vibrationen fest fixiert bleiben.

In[2]:=

bc = {u[0, t] == 0, u[\[Pi], t] == 0};

Geben Sie die Anfangswerte an unterschiedlichen Punkten der Saite an.

In[3]:=

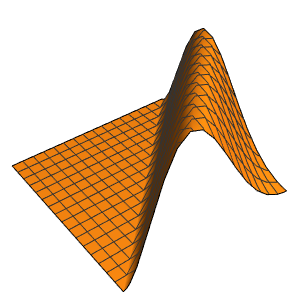
ic = {u[x, 0] == x^2 (\[Pi] - x), \!\(\*SuperscriptBox[\(u\), TagBox[ RowBox[{"(", RowBox[{"0", ",", "1"}], ")"}], Derivative], MultilineFunction->None]\)[x, 0] == 0};

Lösen Sie das Anfangsrandwertproblem.

In[4]:=

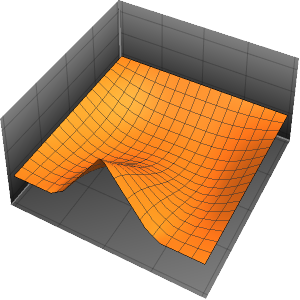
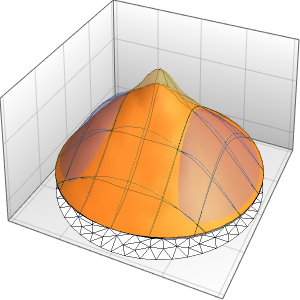
dsol = DSolve[{weqn, bc, ic}, u, {x, t}] /. {K[1] -> m}

Out[4]=

Extrahieren Sie vier Terme von der Inactive-Summe.

In[5]:=

asol[x_, t_] = u[x, t] /. dsol[[1]] /. {\[Infinity] -> 4} // Activate

Out[5]=

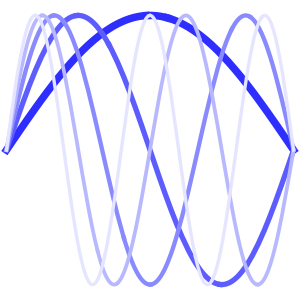
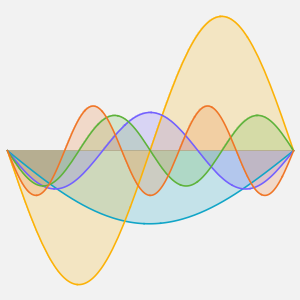
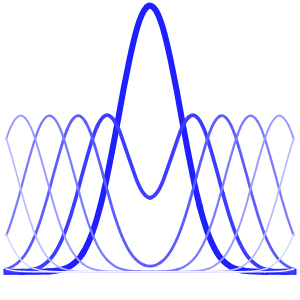
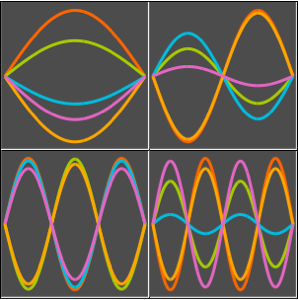
Jeder Term in der Summe repräsentiert eine stehende Welle.

In[6]:=

Table[Show[ Plot[Table[asol[x, t][[m]], {t, 0, 4}] // Evaluate, {x, 0, Pi}, Ticks -> False], ImageSize -> 150], {m, 4}]

Out[6]=

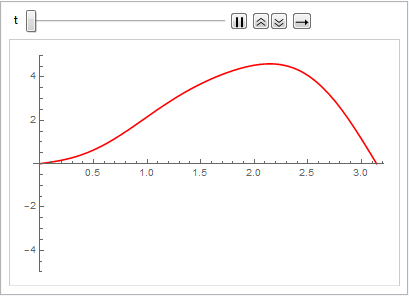
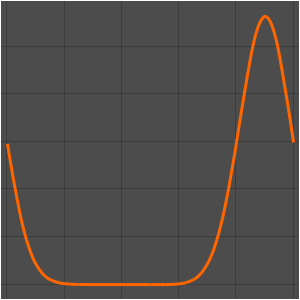
Visualisieren Sie die Vibration der Saite.

In[7]:=

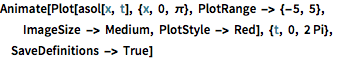
Animate[Plot[asol[x, t], {x, 0, \[Pi]}, PlotRange -> {-5, 5}, ImageSize -> Medium, PlotStyle -> Red], {t, 0, 2 Pi}, SaveDefinitions -> True]

Animation abspielen

Abspielung unterbrechen