Lösen Sie ein Anfangs-Randwertproblem für eine PDE erster Ordnung

Spezifizieren Sie eine lineare partielle Differentialgleichung erster Ordnung.

In[1]:=

eqn = D[u[t, x], t] + D[u[t, x], x] == 0;

Schreiben Sie Anfangs- und Randwertbedingungen für die Gleichung vor.

In[2]:=

ibc = {u[t, 0] == 0, u[0, x] == E^(-x) Sin[x]^2};

Lösen Sie das Problem mit DSolveValue.

In[3]:=

sol = DSolveValue[{eqn, ibc}, u[t, x], {t, x}] // FullSimplify

Out[3]=

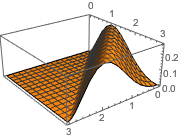
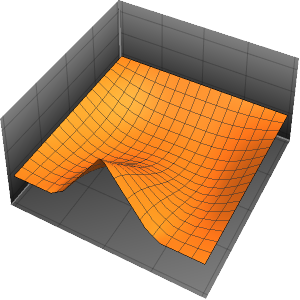
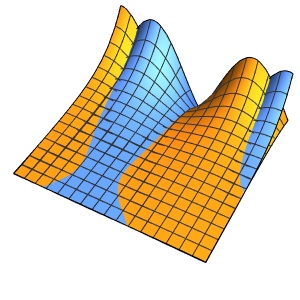
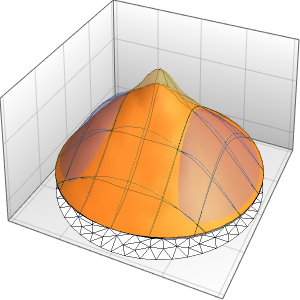
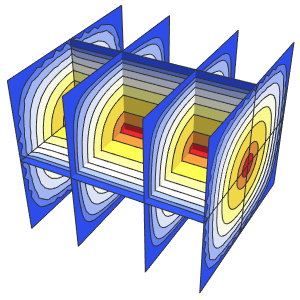
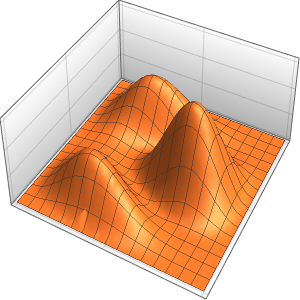
Visualisieren Sie die Lösung.

In[4]:=

Plot3D[sol // Evaluate, {t, 0, 3}, {x, 0, 3}, Exclusions -> None]

Out[4]=