Lösen Sie PDEs mit Ereignissen über Regionen: Neu in Wolfram Language 11

Lösen Sie PDEs mit Ereignissen über Regionen

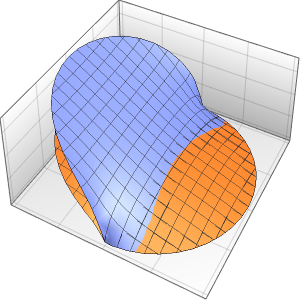
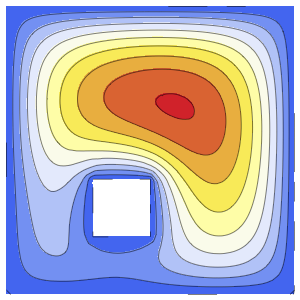
Modellieren Sie eine Thermostat-gesteuerte Wärmeerzeugung in einem Raum mit drei isolierten Wänden und einer Glasfront, die der Außentemperatur ausgesetzt ist.

In[1]:=

\[CapitalOmega] = Rectangle[{0, 0}, {3/2, 1}];
outsideTemp[t_] := 15 + 10*Sin[2 \[Pi] t/24];
kd = 0.78; Ld = 0.05;
\[CapitalGamma] = 
  NeumannValue[Ld/kd*(outsideTemp[t] - u[t, x, y]), {x == 0}];

Eine Heizung wird bei einem Ereignis hoch- oder runtergefahren.

In[2]:=

heaterLoad = 26;
heater[upQ_, t_, tEvent_] := 
 If[upQ == 1, Min[20*Max[(t - tEvent), 0], 1], 
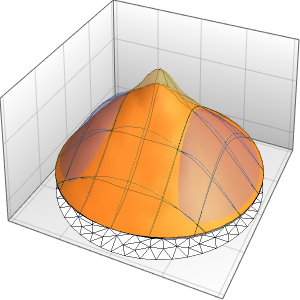
   1 - Min[20*Max[(t - tEvent - 1/8), 0], 1]]*heaterLoad

Die PDE modelliert die Wärmeleitung durch die Luft, während Wärme innerhalb eines Kreises generiert wird und durch das Glasfenster verloren geht.

In[3]:=

\[Rho] = 1.225; Cp = 1005.4;
With[{heating = heater[a[t], t, eventT[t]]},
  pde = D[u[t, x, y], t] - \[Rho]*Cp*Laplacian[u[t, x, y], {x, y}] == 
    If[(x - 1/2)^2 + (y - 1/2)^2 <= (2/10)^2, heating, 
      0] + \[CapitalGamma]];

Wenn das Thermostat an der Stelle eine Temperature über/unter einem Schwellenwert misst und sich die diskrete Variable geändert hat, schaltet sich die Heizung ein bzw. aus.

In[4]:=

triggerLow = 18; triggerHigh = 20;
events = {a[0] == 1, eventT[0] == 0, 
   WhenEvent[
    u[t, 1.25, .25] < 
     triggerLow, {eventT[t], a[t]} -> {If[a[t] == 0, t, eventT[t]], 
      1}], WhenEvent[
    u[t, 1.25, .25] > 
     triggerHigh, {eventT[t], a[t]} -> {If[a[t] == 1, t, eventT[t]], 
      0}]};

Verfolgen Sie die Zeitintegration der PDE mit Anfangsbedingungen, die den Außentemperaturen entsprechen.

In[5]:=

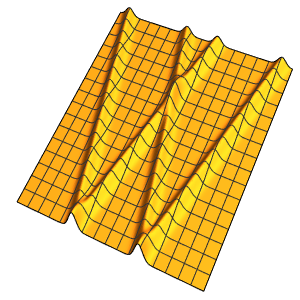
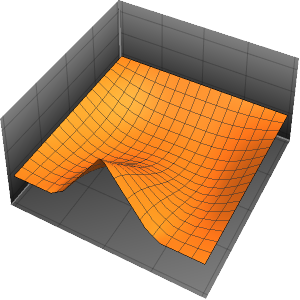
eqn = {pde, u[0, x, y] == outsideTemp[0], events};
res = Monitor[
  NDSolveValue[
   eqn, {u, a}, {t, 0, 2*24}, {x, y} \[Element] \[CapitalOmega], 
   DiscreteVariables -> {eventT[t], a[t]}, 
   EvaluationMonitor :> (monitor = Row[{"t = ", CForm[t]}])], monitor]

Out[5]=

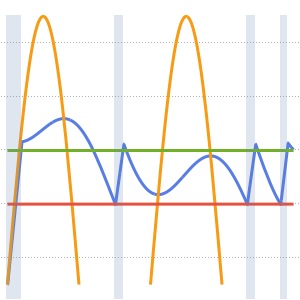
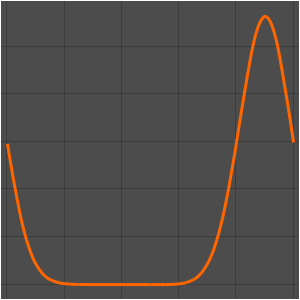
Visualisieren Sie die vom Thermostat gemessene Temperatur, die Außentemperatur, und die Auslöser für die Heizung. Ein blauer Hintergrund bedeutet, dass die Heizung an ist.

In[6]:=

hp = Plot[ 25 res[[2]][t], {t, 0, 2*24}, Filling -> Bottom, 
  PlotStyle -> None]; Show[
 Plot[{res[[1]][t, 1.25, .25], outsideTemp[t], 18, 20}, {t, 0, 
   2*24}], hp]

Out[6]=