Wolfram Language™

Lösen Sie ein Anfangswertproblem für ein lineares hyperbolisches System

Spezifizieren Sie ein inhomogenes lineares hyperbolisches System mit konstanten Koeffizienten.

In[1]:=

eqns = {D[u[x, t], t] == D[v[x, t], x] + 1, D[v[x, t], t] == -D[u[x, t], x] - 1};

Geben Sie Anfangsbedingungen für das System an.

In[2]:=

ic = {u[x, 0] == Cos[x]^2, v[x, 0] == Sin[x]};

Lösen Sie das System mit DSolveValue.

In[3]:=

sol = DSolveValue[{eqns, ic}, {u[x, t], v[x, t]}, {x, t}] // FullSimplify

Out[3]=

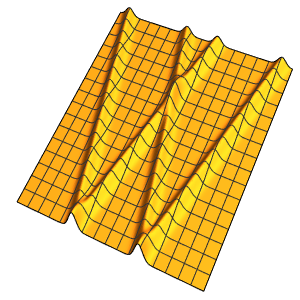
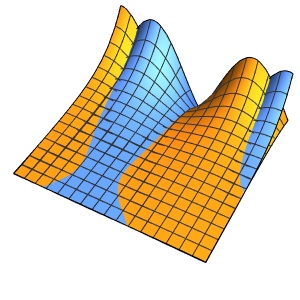
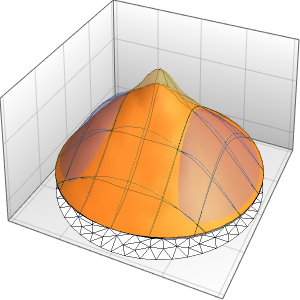
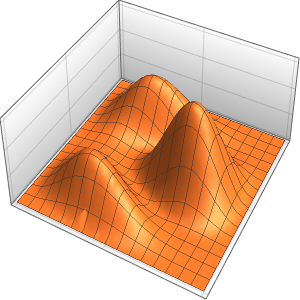
Visualisieren Sie die Lösung.

In[4]:=

Plot3D[sol // Evaluate, {x, 0, 4}, {t, 0, 3}, PlotRange -> {-70, 120}]

Out[4]=