Distribución truncada con cantidades
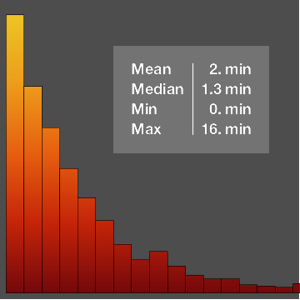
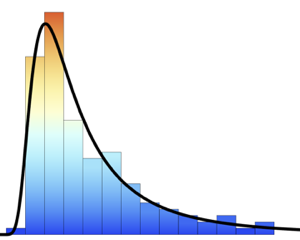
El diámetro de un arándano americano sigue una distribución normal con media de 16 mm y desviación típica de 1.6 mm. Un fruta debe ser de al menos 15 mm de diámetro para ser vendida completa; de lo contrario se usa para fabricar salsa de arándanos. Encuentre la distribución de tamaño de las frutas que se venden completas.
In[1]:=
cran\[ScriptCapitalD] =
NormalDistribution[Quantity[16, "Millimeters"],
Quantity[1.6, "Millimeters"]];
\[ScriptCapitalD] =
TruncatedDistribution[{Quantity[15, "Millimeters"], \[Infinity]},
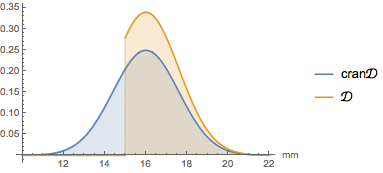
cran\[ScriptCapitalD]];Compare las funciones de densidad de probabilidad.
In[2]:=

Plot[{PDF[cran\[ScriptCapitalD], Quantity[x, "Milimeters"]],
PDF[\[ScriptCapitalD], Quantity[x, "Milimeters"]]}, {x, 10, 22},
PlotLegends -> {"cran\[ScriptCapitalD]", "\[ScriptCapitalD]"},
Filling -> Axis, AxesLabel -> {"mm"}]Out[2]=
Asumiendo que un paquete de una libra de arándanos tiene un volumen de alrededor de 30 in3, encuentre los límites de promedio inferior y superior para el número de arándanos en dicho paquete.
In[3]:=

lowerbound =
Floor[NExpectation[
Divide[Quantity[30, "Inches"^3],
Volume[Cuboid[{0, 0, 0}, {x, x, x}]]],
x \[Distributed] \[ScriptCapitalD]]]Out[3]=
In[4]:=

upperbound =
Ceiling[NExpectation[
Divide[Quantity[30, "Inches"^3], Volume[Ball[{0, 0, 0}, x/2]]],
x \[Distributed] \[ScriptCapitalD]]]Out[4]=