Wolfram Language™

Orden de distribución a partir de distribución con unidades

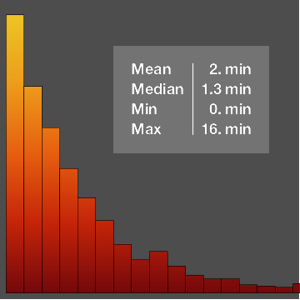
Un sistema tiene tres componentes, de los cuales uno es primario y dos son redundantes. Cada componente tiene una vida útil siguiendo una WeibullDistribution, con parámetro de forma de 2 y una media de vida útil de 885 horas.

In[1]:=

{sol} = NSolve[ Mean[WeibullDistribution[2, b]] == Quantity[885, "Hours"], b]

Out[1]=

In[2]:=

\[ScriptD] = WeibullDistribution[2, b] /. sol

Out[2]=

La vida útil de este sistema puede ser descrito como la máxima vida útil de sus componentes.

In[3]:=

\[ScriptCapitalD] = OrderDistribution[{\[ScriptD], 3}, 3]

Out[3]=

La media de vida útil del sistema.

In[4]:=

Mean[\[ScriptCapitalD]]

Out[4]=

Compare con el cálculo usando ReliabilityDistribution.

In[5]:=

Mean[ReliabilityDistribution[ comp1 \[Or] comp2 \[Or] comp3, {{comp1, \[ScriptD]}, {comp2, \[ScriptD]}, {comp3, \ \[ScriptD]}}]]

Out[5]=

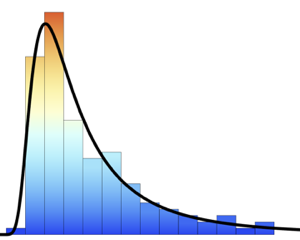
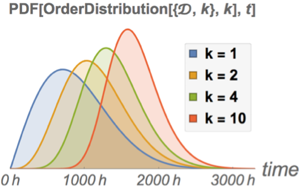
Compare la función de densidad de probabilidad de vida útil de un solo componente con la del sistema.

In[6]:=

Plot[{PDF[\[ScriptD], Quantity[x, "Hours"]], PDF[\[ScriptCapitalD], Quantity[x, "Hours"]]}, {x, 0, 3000}, FrameLabel -> {"hr"}, PlotTheme -> "Detailed", PlotLegends -> {"single component", "system"}, PlotLabel -> "Lifetime Distribution Density"]

Out[6]=