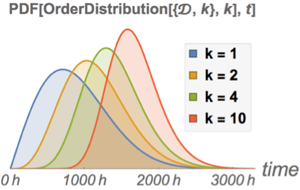
수량 모수의 분포
평균 70인치, 표준 편차 6.5 인치의 정규 분포에서 신장 분포의 근사치를 구합니다. 분포는 Quantity를 대응하는 평균과 표준 편차의 모수로 사용하여 구축할 수 있으며, 적절한 QuantityDistribution을 반환합니다.
In[1]:=
height\[ScriptCapitalD] =
NormalDistribution[Quantity[70, "Inches"], Quantity[6.5, "Inches"]]Out[1]=
분포는 지정된 단위로 확률 변수를 나타냅니다.
In[2]:=
averageHeight = Mean[height\[ScriptCapitalD]]Out[2]=
적절한 수량 인수를 사용하여 분포의 계산을 실시합니다.
In[3]:=
CDF[height\[ScriptCapitalD], Quantity[170, "Centimeters"]]Out[3]=
어떤 사람이 65인치에서 72인치 사이의 신장을 가질 확률을 계산합니다.
In[4]:=
Probability[Quantity[65, "in"] < x < Quantity[72, "in"],
x \[Distributed] height\[ScriptCapitalD]]Out[4]=
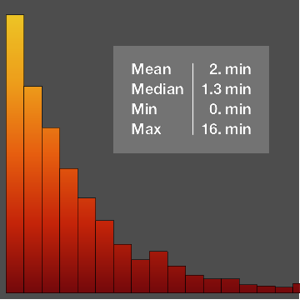
이 키의 분포를 가정하여 모자가 사람의 머리에서 바닥에 떨어질 때까지의 평균 시간을 구합니다.
In[5]:=

NExpectation[Sqrt[(2 h)/Entity["Planet", "Earth"]["Gravity"]],
h \[Distributed] height\[ScriptCapitalD]]Out[5]=