Wolfram言語™

DysonのCoulombガス

CircularOrthogonalMatrixDistributionに従う行列の固有値の結合分布は，逆温度が 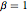である円上のDysonのCoulombガスのBoltzmann分布と一致する．粒子あたりの平均ハミルトニアン（運動項は含まない）を定義する．

In[1]:=

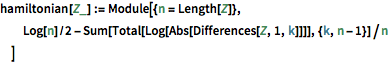
hamiltonian[Z_] := Module[{n = Length[Z]}, Log[n]/2 - Sum[Total[Log[Abs[Differences[Z, 1, k]]]], {k, n - 1}]/n ]

ハミルトニアンの分布を定義する．

In[2]:=

h\[ScriptCapitalD] = MatrixPropertyDistribution[hamiltonian[Eigenvalues[x]], x \[Distributed] CircularOrthogonalMatrixDistribution[n]];

さまざまな大きさの系のハミルトニアンのサンプルの平均を計算する．

In[3]:=

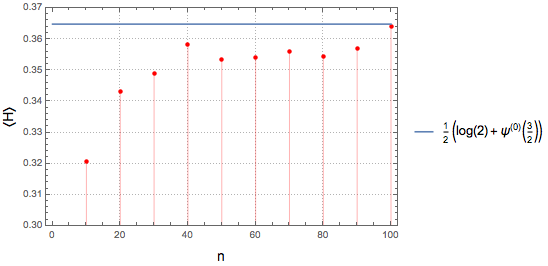
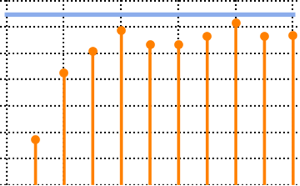
means = Table[{n, Mean[RandomVariate[h\[ScriptCapitalD], 1000]]}, {n, 10, 100, 10}];

サンプル平均をプロットし，熱力学的限界と比較する．

In[4]:=

Show[ListPlot[means, PlotStyle -> {Red, PointSize[Medium]}, Filling -> Axis, PlotRange -> {0.3, 0.37}, FrameLabel -> {Style["n", Black, 14], Style["\[LeftAngleBracket]H\[RightAngleBracket]", Black, 14]}, PlotTheme -> "Detailed"], Plot[1/2 (Log[2] + PolyGamma[0, 3/2]), {x, 0, 100}, PlotTheme -> "Detailed"]]

Out[4]=