Wishart and Inverse Wishart Distributions

The Wishart distribution is the distribution of the covariance matrix of samples drawn from independent multinormal random vectors. It is a generalization of 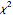distribution to multiple dimensions. The distribution appears naturally in multivariate statistics such as regression, covariance, etc.

Generate a random positive definitive matrix to use as parameters for the Wishart distribution.

In[1]:=

\[CapitalSigma] = DiagonalMatrix[RandomReal[10, 5]];

Matrices from the Wishart distribution are symmetric and positive definite. »

In[2]:=

dist = WishartMatrixDistribution[30, \[CapitalSigma]]; mat = RandomVariate[dist];

In[3]:=

SymmetricMatrixQ[mat] && PositiveDefiniteMatrixQ[mat]

Out[3]=

Inverse Wishart distribution is the distribution of the inverse matrices from the Wishart distribution. »

In[4]:=

invdist = InverseWishartMatrixDistribution[30, Inverse[\[CapitalSigma]]]; invmat = RandomVariate[invdist];

Matrices from the inverse Wishart distribution are symmetric and positive definite.

In[5]:=

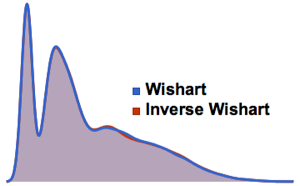
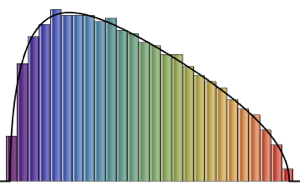
SymmetricMatrixQ[invmat] && PositiveDefiniteMatrixQ[invmat]

Out[5]=

Compare the distribution of eigenvalues for matrices from the Wishart and inverse Wishart distributions.

In[6]:=

eigs = Flatten[ RandomVariate[ MatrixPropertyDistribution[Eigenvalues[x], x \[Distributed] dist], 10^4]]; inveigs = Flatten[RandomVariate[ MatrixPropertyDistribution[Eigenvalues[x]^-1, x \[Distributed] invdist], 10^4]];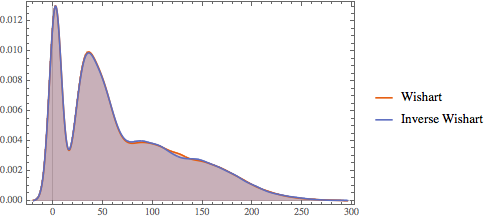

In[7]:=

SmoothHistogram[{eigs, inveigs}, PlotLegends -> {"Wishart", "Inverse Wishart"}, Filling -> Axis, ImageSize -> Medium, PlotTheme -> "Scientific"]

Out[7]=

For any nonzero vector 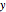and Wishart matrix 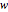with scale matrix 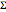, the statistic 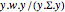is 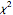distributed.

In[8]:=

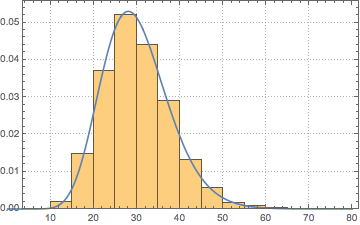
y = #/Sqrt[#.\[CapitalSigma].#] &[RandomReal[1, 5]]; data = RandomVariate[ MatrixPropertyDistribution[y.w.y, w \[Distributed] WishartMatrixDistribution[30, \[CapitalSigma]]], 10^4];

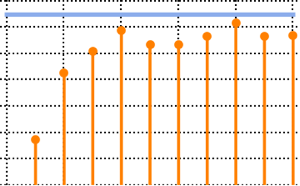
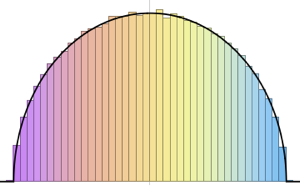
In[9]:=

Show[Histogram[data, Automatic, PDF, PlotTheme -> "Detailed"], Plot[PDF[ChiSquareDistribution[30], x], {x, 0, 80}], ImageSize -> Medium]

Out[9]=