Longest Increasing Subsequences

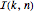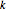The number of permutations of elements in which the longest increasing subsequence is at most of length can be computed by averaging over 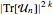, where 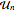are matrices drawn from CircularUnitaryMatrixDistribution of dimension .

In[1]:=

{k, n} = {6, 2};

Define the matrix property distribution and calculate the mean.

In[2]:=

\[ScriptCapitalD] = MatrixPropertyDistribution[Abs[Tr[\[ScriptCapitalU]]]^( 2 k), \[ScriptCapitalU] \[Distributed] CircularUnitaryMatrixDistribution[n]]; N[Mean[\[ScriptCapitalD]]]

Out[2]=

Compare with the direct count.

In[3]:=

Count[Permutations[Range[k]], perm_ /; Length[LongestOrderedSequence[perm]] <= n]

Out[3]=

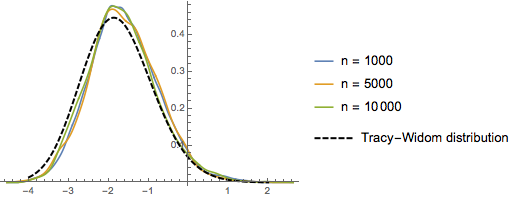
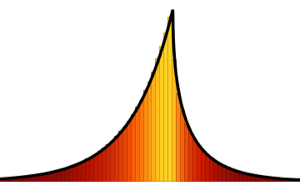
For 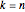, the distribution of the scaled lengths of the longest increasing subsequences of random permutations converges to the Tracy–Widom distribution with .

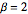In[4]:=

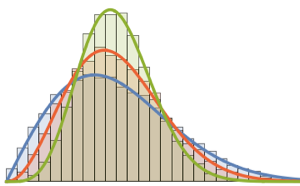
sample[n_] := 1/n^(1/6) (Table[ Length[LongestOrderedSequence[ RandomSample[Range[n]]]], {2000}] - 2.0 Sqrt[n]);

Compare the smooth histogram of sampled scaled lengths for increasing dimensions with the PDF of the Tracy–Widom distribution.

In[5]:=

dims = {1000, 5000, 10000}; Show[ SmoothHistogram[sample /@ dims, PlotLegends -> (Row[{"n = ", #}] & /@ dims)], Plot[PDF[TracyWidomDistribution[2], x], {x, -4, 2}, PlotStyle -> {Black, Dashed, Thick}, PlotLegends -> {"Tracy-Widom distribution"}]]

Out[5]=