Wolfram 语言™

戴森库仑气体

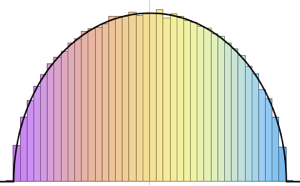
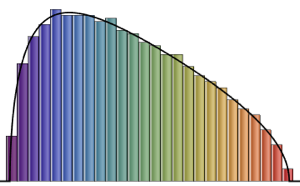
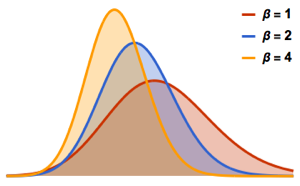
服从 CircularOrthogonalMatrixDistribution 的矩阵特征值的联合分布等价于戴森库仑气体在圆上的玻尔兹曼分布，其中温度倒数 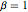. 定义每个粒子的平均哈密顿量（无动能项）.

In[1]:=

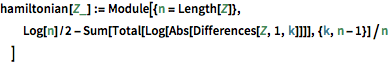
hamiltonian[Z_] := Module[{n = Length[Z]}, Log[n]/2 - Sum[Total[Log[Abs[Differences[Z, 1, k]]]], {k, n - 1}]/n ]

定义哈密顿分布.

In[2]:=

h\[ScriptCapitalD] = MatrixPropertyDistribution[hamiltonian[Eigenvalues[x]], x \[Distributed] CircularOrthogonalMatrixDistribution[n]];

计算不同大小的系统的哈密顿样本均值.

In[3]:=

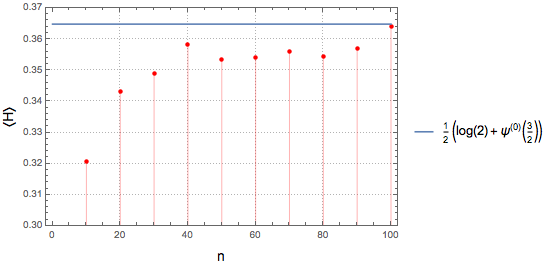
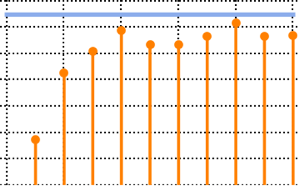
means = Table[{n, Mean[RandomVariate[h\[ScriptCapitalD], 1000]]}, {n, 10, 100, 10}];

绘制样本均值，并将它们与热力学极限比较.

In[4]:=

Show[ListPlot[means, PlotStyle -> {Red, PointSize[Medium]}, Filling -> Axis, PlotRange -> {0.3, 0.37}, FrameLabel -> {Style["n", Black, 14], Style["\[LeftAngleBracket]H\[RightAngleBracket]", Black, 14]}, PlotTheme -> "Detailed"], Plot[1/2 (Log[2] + PolyGamma[0, 3/2]), {x, 0, 100}, PlotTheme -> "Detailed"]]

Out[4]=