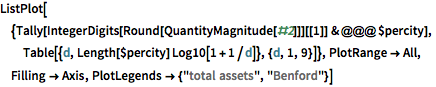連邦預金保険公社の組織データ
連邦預金保険公社(FDIC)は,国内の金融機関の預金に責任を持つ合衆国政府の独立した機関である.現在のところ,加盟機関の預金は25万ドルまで保証されている.ここでは,加盟金融機関の債権,大きさの分布,地理的散らばりを調べる.
まず,FDICデータの実体ストアをResourceObjectとしてロードする.
In[1]:=
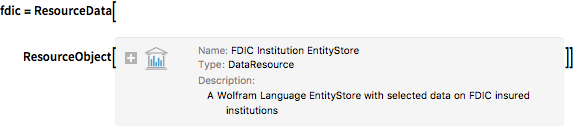
fdic = ResourceData[
ResourceObject[
Association[
"Name" -> "FDIC Institution EntityStore",
"UUID" -> "6f5d37d4-1406-483c-b67c-f58d903d16b1",
"ResourceType" -> "DataResource", "Version" -> "1.0.0",
"Description" -> "A Wolfram Language EntityStore with selected \
data on FDIC insured institutions",
"ContentSize" -> Quantity[0, "Bytes"],
"ContentElements" -> {"EntityStore"}]]]Out[1]=

このセッションのためにストアを登録する.
In[2]:=
PrependTo[$EntityStores, fdic];FDICの加盟金融機関数を数える.
In[3]:=
Length[ents = EntityList["FDICInstitution"]]Out[3]=
実体ストアの使用可能な特性をいくつかリストにする.
In[4]:=
EntityProperties["FDICInstitution"] // Sort // Take[#, 20] &Out[4]=

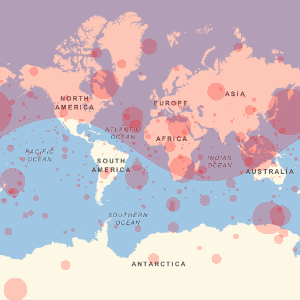
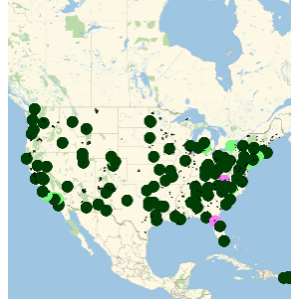
FDICの加盟銀行の地理的位置を可視化する.
In[5]:=
GeoListPlot[EntityList["FDICInstitution"], PlotMarkers -> "$"]Out[5]=
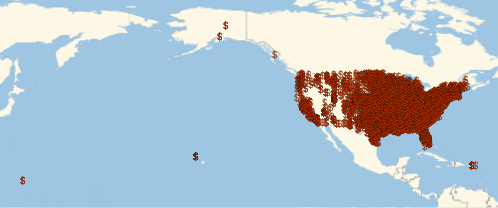
階数分布を両対数プロットで表示する.
In[6]:=
ListLogLogPlot[
Reverse@Sort[EntityValue["FDICInstitution", "TotalAssets"]],
AxesLabel -> Automatic, PlotStyle -> PointSize[Medium]]Out[6]=
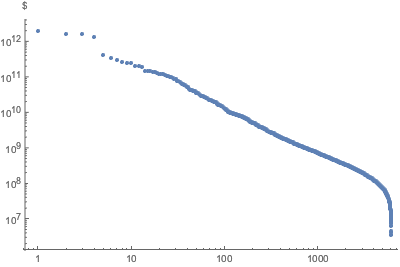
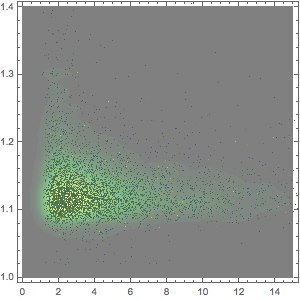
従業員数と資産をプロットする.
In[7]:=
empVsAssets =
EntityValue[
"FDICInstitution", {"TotalEmployeeNumber", "TotalAssets"}];In[8]:=
ListLogLogPlot[empVsAssets, AxesLabel -> Automatic]Out[8]=
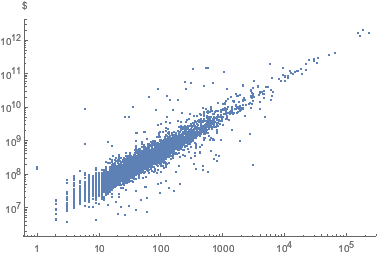
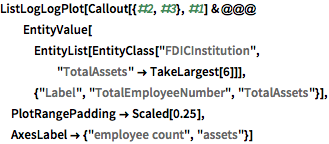
規模が最も大きい6つの機関にラベルを付ける.
完全なWolfram言語入力を表示する
Out[9]=
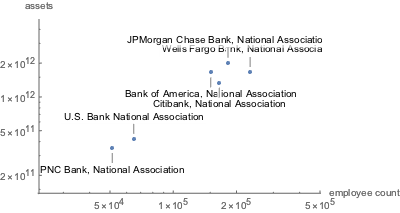
負債と資産をプロットする.
In[10]:=
assetsVsLiability =
EntityValue["FDICInstitution", {"TotalAssets", "TotalLiabilities"}];In[11]:=
ListLogLogPlot[assetsVsLiability, AxesLabel -> Automatic]Out[11]=
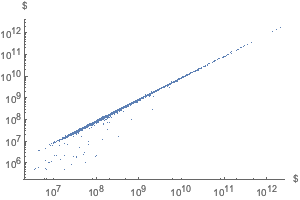
貸出し総額,借入れ総額,総預金量を適合度とともにプロットする.
In[12]:=
loanVsDeposit =
EntityValue[
"FDICInstitution", {"NetLoansAndLeases", "TotalDeposits"}];In[13]:=
nmf = NonlinearModelFit[
Select[QuantityMagnitude /@ loanVsDeposit, Min[#] > 0 &],
c + a x^\[Alpha], {a, \[Alpha], c}, x]Out[13]=
In[14]:=
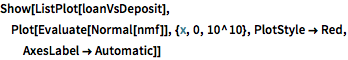
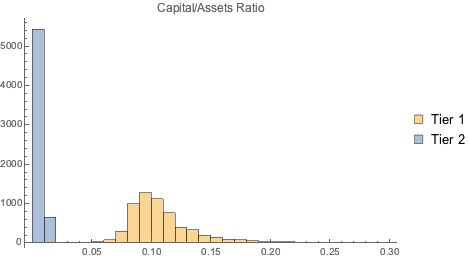
Show[ListPlot[loanVsDeposit],
Plot[Evaluate[Normal[nmf]], {x, 0, 10^10}, PlotStyle -> Red,
AxesLabel -> Automatic]]Out[14]=
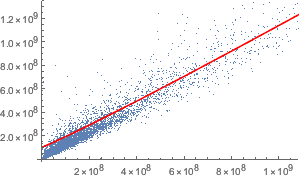
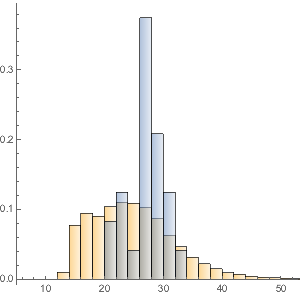
中核的自己資本(安全)と補完的自己資本(リスクが大きい)を総資産と比較する.
In[15]:=

{tierOneCapitalToAssets,
tierTwoCapitalToAssetsCapitalToAssets} = (Divide @@@
EntityValue[
"FDICInstitution", {#, "TotalAssets"}]) & /@ {"TierOneCapital",
"TierTwoRiskBasedCapital"};In[16]:=

Histogram[{tierOneCapitalToAssets,
tierTwoCapitalToAssetsCapitalToAssets}, {0, 0.3, 0.01},
ChartLegends -> {"Tier 1", "Tier 2"},
PlotLabel -> "Capital/Assets Ratio"]Out[16]=
資産の分布を"EntityAssociation"として取り出す.
In[17]:=
dat = EntityValue["FDICInstitution", "TotalAssets",
"EntityAssociation"];資産の分布をプロットする.
In[18]:=
Histogram[dat, "Log", AxesLabel -> Automatic]Out[18]=
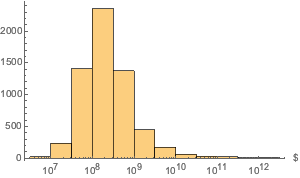
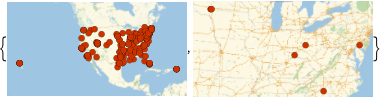
資産が50億ドルを超える銀行と3000億ドルを超える銀行の位置を表示する.
In[19]:=
GeoListPlot[
Keys[Select[dat,
GreaterThan[Quantity[#, "USDollars"]]]]] & /@ {5*^9, 300*^9}Out[19]=
上位10行が残りの6121行を合わせたよりも多くの資産を有することをグラフィカルに示す.
完全なWolfram言語入力を表示する
Out[20]=
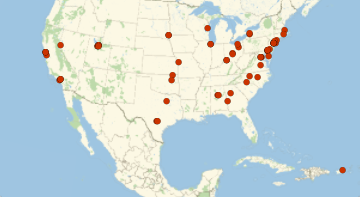
預金量が上位1%の銀行を求める.
In[21]:=
dat1 = EntityValue["FDICInstitution", "TotalDeposits",
"EntityAssociation"];In[22]:=
{bottom1percent, top1percent} =
Quantile[values = Values[dat1], {0.01, 0.99}]Out[22]=
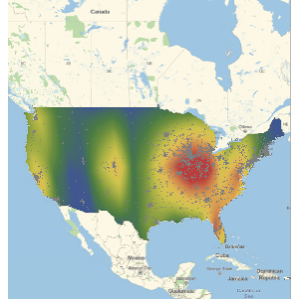
地図上にプロットする.
In[23]:=
GeoListPlot[Keys[Select[dat1, GreaterThan[top1percent]]]]Out[23]=
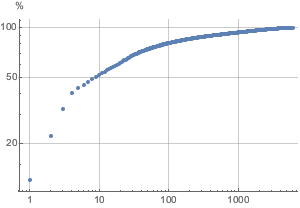
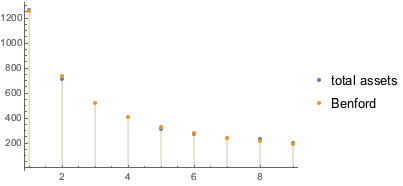
都市に対する資産の分布はBenfordの法則と驚くほど一致する.
完全なWolfram言語入力を表示する
Out[25]=
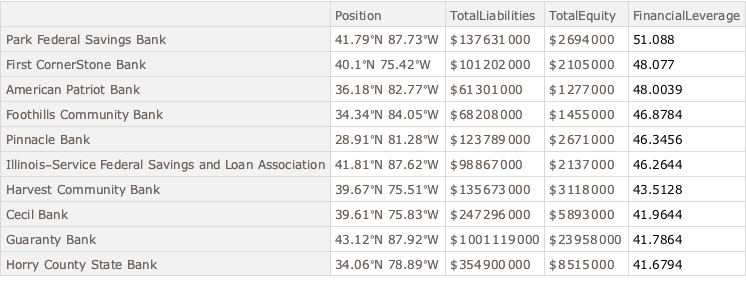
財務レバレッジが最高の銀行を示す.
完全なWolfram言語入力を表示する
In[27]:=
dataSet3[TakeLargestBy["FinancialLeverage", 10]]Out[27]=
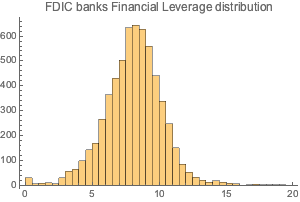
財務レバレッジの分布をプロットする.
In[28]:=
Histogram[dataSet3[All, "FinancialLeverage"], {0, 20, 0.5},
PlotLabel -> "FDIC banks Financial Leverage distribution"]Out[28]=
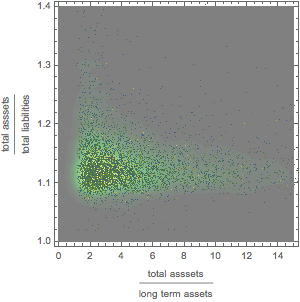
資産,長期資産,債務の関係をグラフィカルに調べる.
完全なWolfram言語入力を表示する
Out[33]=