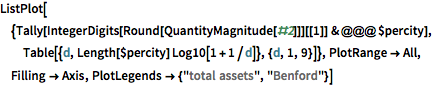Wolfram Language™

Institutsdaten der Federal Deposit Insurance Corporation

Die Federal Deposit Insurance Corporation (FDIC) ist eine unabhängige US-Regierungsbehörde und Einlagensicherungsfonds. Derzeit werden Einlagen in Mitgliedsinstitutionen bis zu einer Höhe von 250.000$ versichert. In diesem Beispiel werden der Aktienbesitz, die Größenverteilung und die geographische Verteilung von Mitgliedsinstitutionen untersucht.

Laden Sie als ersten Schritt einen Entity-Store mit FDIC-Daten als ResourceObject.

In[1]:=

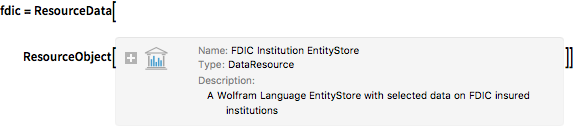
fdic = ResourceData[ ResourceObject[ Association[ "Name" -> "FDIC Institution EntityStore", "UUID" -> "6f5d37d4-1406-483c-b67c-f58d903d16b1", "ResourceType" -> "DataResource", "Version" -> "1.0.0", "Description" -> "A Wolfram Language EntityStore with selected \ data on FDIC insured institutions", "ContentSize" -> Quantity[0, "Bytes"], "ContentElements" -> {"EntityStore"}]]]

Out[1]=

Registrieren Sie den Store für diese Sitzung.

In[2]:=

PrependTo[$EntityStores, fdic];

Ermitteln Sie die Anzahl bestehender FDIC-Institutionen.

In[3]:=

Length[ents = EntityList["FDICInstitution"]]

Out[3]=

Machen Sie eine Liste verfügbarer Eigenschaften des EntityStore.

In[4]:=

EntityProperties["FDICInstitution"] // Sort // Take[#, 20] &

Out[4]=

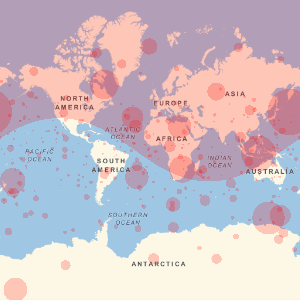
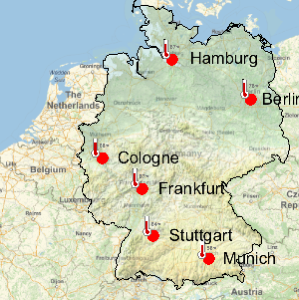
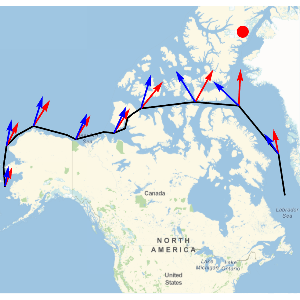
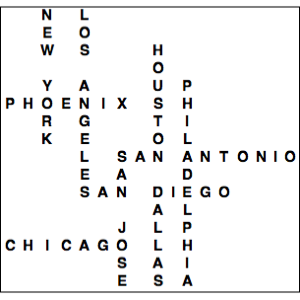
Visualisieren Sie die geographischen Standpunkte der Banken.

In[5]:=

GeoListPlot[EntityList["FDICInstitution"], PlotMarkers -> "$"]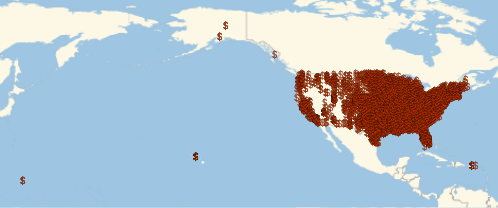

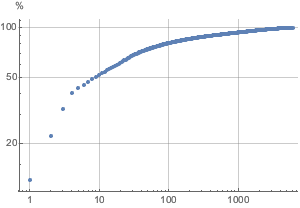
Out[5]=

Stellen Sie die Rangverteilung in einem doppelt logarithmischen Plot dar.

In[6]:=

ListLogLogPlot[ Reverse@Sort[EntityValue["FDICInstitution", "TotalAssets"]], AxesLabel -> Automatic, PlotStyle -> PointSize[Medium]]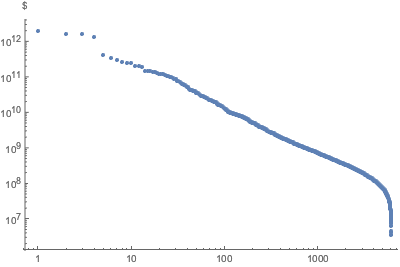

Out[6]=

Visualisieren Sie Angestellte vs. verwaltetes Vermögen.

In[7]:=

empVsAssets = EntityValue[ "FDICInstitution", {"TotalEmployeeNumber", "TotalAssets"}];

In[8]:=

ListLogLogPlot[empVsAssets, AxesLabel -> Automatic]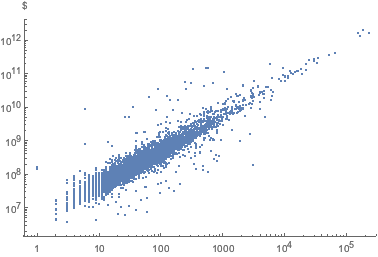

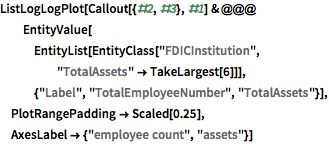
Out[8]=

Fügen Sie Beschriftungen für die sechs größten Institutionen ein.

In[9]:=

ListLogLogPlot[ Callout[{#2, #3}, #1] & @@@ EntityValue[ EntityList[ EntityClass["FDICInstitution", "TotalAssets" -> TakeLargest[6]]], {"Label", "TotalEmployeeNumber", "TotalAssets"}], PlotRangePadding -> Scaled[0.25], AxesLabel -> {"employee count", "assets"}]

Out[9]=

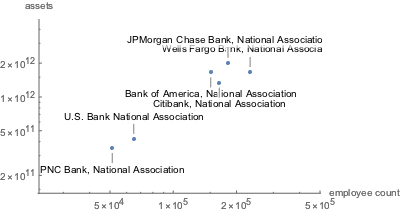
Visualisieren Sie Verbindlichkeiten vs. Vermögen.

In[10]:=

assetsVsLiability = EntityValue["FDICInstitution", {"TotalAssets", "TotalLiabilities"}];

In[11]:=

ListLogLogPlot[assetsVsLiability, AxesLabel -> Automatic]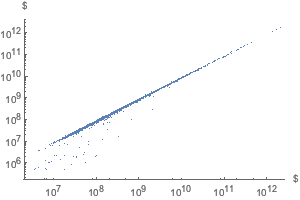

Out[11]=

Visualisieren Sie Nettodarlehen und Miete bzw. Pacht vs. Gesamteinlagen in Verbindung mit einem Modell.

In[12]:=

loanVsDeposit = EntityValue[ "FDICInstitution", {"NetLoansAndLeases", "TotalDeposits"}];

In[13]:=

nmf = NonlinearModelFit[ Select[QuantityMagnitude /@ loanVsDeposit, Min[#] > 0 &], c + a x^\[Alpha], {a, \[Alpha], c}, x]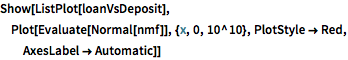

Out[13]=

In[14]:=

Show[ListPlot[loanVsDeposit], Plot[Evaluate[Normal[nmf]], {x, 0, 10^10}, PlotStyle -> Red, AxesLabel -> Automatic]]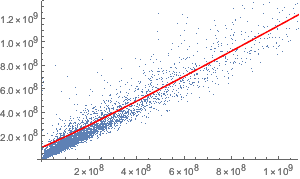

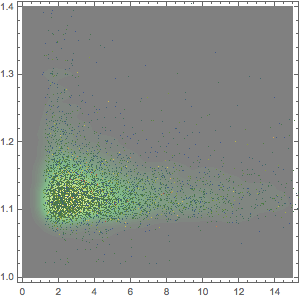
Out[14]=

Vergleichen Sie Tier 1 (hartes Kernkapital, sicher) und Tier 2 (Ergänzungskapital, riskanter) mit den Vermögensgesamtwerten.

In[15]:=

{tierOneCapitalToAssets, tierTwoCapitalToAssetsCapitalToAssets} = (Divide @@@ EntityValue[ "FDICInstitution", {#, "TotalAssets"}]) & /@ {"TierOneCapital", "TierTwoRiskBasedCapital"};

In[16]:=

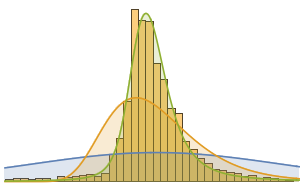
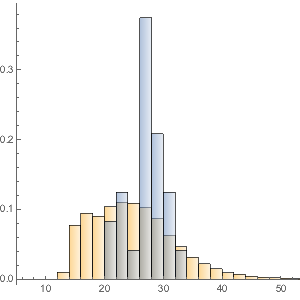
Histogram[{tierOneCapitalToAssets, tierTwoCapitalToAssetsCapitalToAssets}, {0, 0.3, 0.01}, ChartLegends -> {"Tier 1", "Tier 2"}, PlotLabel -> "Capital/Assets Ratio"]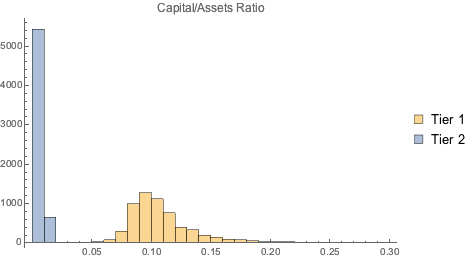

Out[16]=

Ermitteln Sie die Vermögensverteilung als "EntityAssociation".

In[17]:=

dat = EntityValue["FDICInstitution", "TotalAssets", "EntityAssociation"];

Visualisieren Sie die Vermögensverteilung.

In[18]:=

Histogram[dat, "Log", AxesLabel -> Automatic]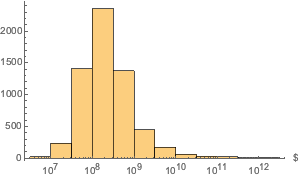

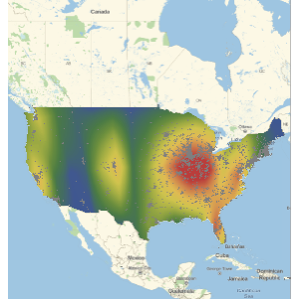
Out[18]=

Zeigen Sie die Standorte von Banken mit Vermögenswerten von mehr als 5 Milliarden und 300 Milliarden Dollar an.

In[19]:=

GeoListPlot[ Keys[Select[dat, GreaterThan[Quantity[#, "USDollars"]]]]] & /@ {5*^9, 300*^9}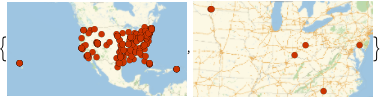

Out[19]=

Sie sehen deutlich, dass die Top 10 Banken mehr Vermögenswerte besitzen als die restlichen 6121 zusammen.

In[20]:=

With[{atas = QuantityMagnitude[ EntityValue["FDICInstitution", EntityProperty["FDICInstitution", "AverageTotalAssets"]]]}, ListLogLogPlot[100 Accumulate[Reverse[Sort[atas]]]/Total[atas], PlotRange -> All, GridLines -> Automatic, PlotStyle -> PointSize[Medium], AxesLabel -> {None, Quantity[None, "Percent"]}]]

Out[20]=

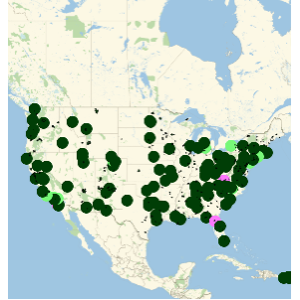
Ermitteln Sie die Banken mit dem höchsten Prozent (1%) an Einlagen.

In[21]:=

dat1 = EntityValue["FDICInstitution", "TotalDeposits", "EntityAssociation"];

In[22]:=

{bottom1percent, top1percent} = Quantile[values = Values[dat1], {0.01, 0.99}]

Out[22]=

Visualisieren Sie diese auf einer Karte.

In[23]:=

GeoListPlot[Keys[Select[dat1, GreaterThan[top1percent]]]]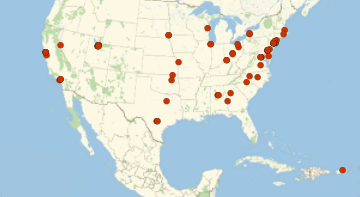

Out[23]=

Die Verteilung der Vermögenswerte pro Stadt entspricht dem Benfordschen Gesetz bis zu einem bemerkenswerten Grad.

In[24]:=

$percity = Reverse[SortBy[{#[[1, 1]], Total[#[[All, -1]]]} & /@ Normal[Normal[ DeleteMissing[ SortBy[GroupBy[ EntityValue["FDICInstitution", {"City", "TotalAssets"}], First] , Length], 1, 3]][[All, -1]]], Last]];

In[25]:=

ListPlot[{Tally[ IntegerDigits[Round[QuantityMagnitude[#2]]][[1]] & @@@ $percity], Table[{d, Length[$percity] Log10[1 + 1/d]}, {d, 1, 9}]}, PlotRange -> All, Filling -> Axis, PlotLegends -> {"total assets", "Benford"}]

Out[25]=

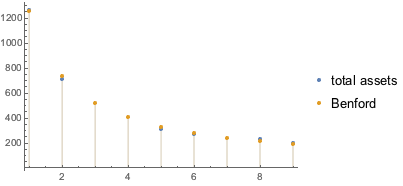
Zeigen Sie die Banken mit der größten Kapitalstruktur an.

In[26]:=

dataSet3 = Append[#, <| "FinancialLeverage" -> N[#TotalLiabilities/#TotalEquity]|>] & /@ EntityValue[ "FDICInstitution", {"Position", "TotalLiabilities", "TotalEquity"}, "Dataset"];

In[27]:=

dataSet3[TakeLargestBy["FinancialLeverage", 10]]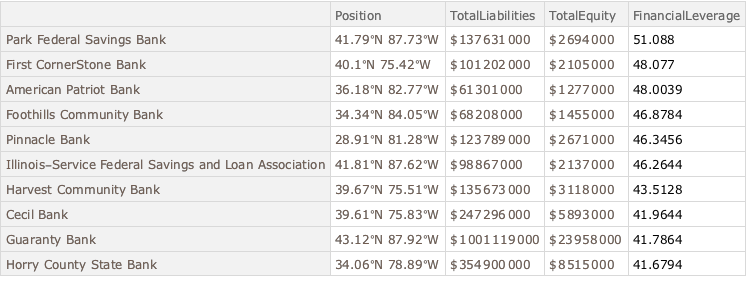

Out[27]=

Plotten Sie die Verteilung der Kapitalstruktur.

In[28]:=

Histogram[dataSet3[All, "FinancialLeverage"], {0, 20, 0.5}, PlotLabel -> "FDIC banks Financial Leverage distribution"]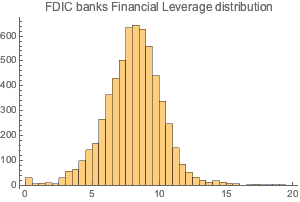

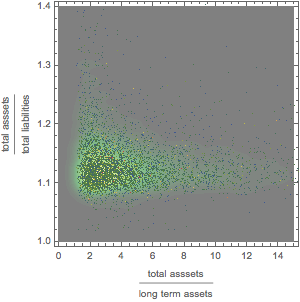
Out[28]=

Untersuchen Sie graphisch die Beziehung zwischen Vermögen, Anlagevermögen und Verbindlichkeiten.

In[29]:=

props = {EntityProperty["FDICInstitution", "TotalAssets"], EntityProperty["FDICInstitution", "LongTermAssets"], EntityProperty["FDICInstitution", "TotalLiabilities"]}; data = Select[ N@QuantityMagnitude@ DeleteMissing[ EntityValue["FDICInstitution", Append[props, "Entity"]], 1, 2], Min[Most[#]] > 0 &];

In[30]:=

data2 = Select[{#1/#2, #1/#3, #4} & @@@ data, Between[{0, 15}][#[[1]]] && Between[{1, 1.4}][#[[2]]] &];

In[31]:=

sdk = SmoothKernelDistribution[Most /@ data2];

In[32]:=

label[{a_, b_, c_, _[d_]}] := Column[{d, Grid[Transpose[{props, Quantity[NumberForm[#, 4], "USDollars"] & /@ {a, b, c}}], Dividers -> Center]}]

In[33]:=

ContourPlot[PDF[sdk, {x, y}], {x, 0, 15}, {y, 1, 1.4}, PlotRange -> All, Contours -> 50, ContourStyle -> None, ColorFunction -> (Lighter[ColorData["AvocadoColors"][#], 0.5] &), FrameLabel -> {"total asssets"/"long term assets", "total asssets"/"total liabilities"}, Epilog -> ({ColorData["DarkRainbow"][(Log10[#1] - 7)/5], PointSize[0.00125], Point[{#1/#2, #1/#3}]} & @@@ data)]

Out[33]=