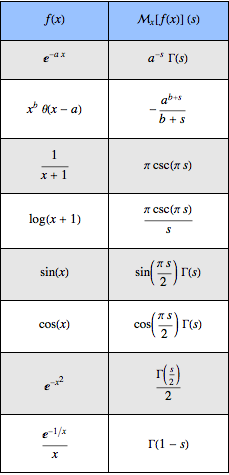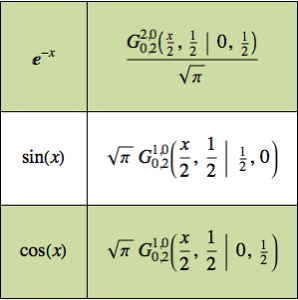メリン(Mellin)変換を計算する: Wolfram言語 11の新機能

‹›

メリン(Mellin)変換を計算する

MellinTransformを使って，関数のメリン変換を計算する．

In[1]:=

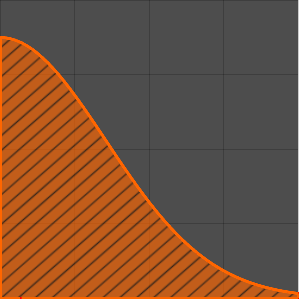
MellinTransform[E^(-a x), x, s]

Out[1]=

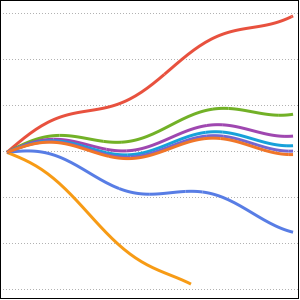
異なる値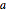に対する結果をプロットする．

In[2]:=

MellinTransform[E^(-a x), x, s];
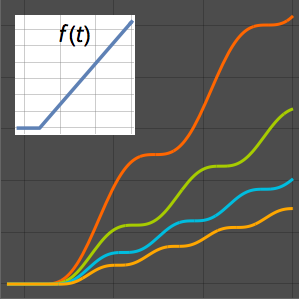
Plot[Table[% , {a, 1, 2, 1/4}] // Evaluate, {s, 0, 4}]

Out[2]=

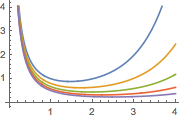
結果の妥当性に対する条件を生成する．

In[3]:=

MellinTransform[E^(-a x), x, s, GenerateConditions -> True]

Out[3]=

多変量のメリン変換を計算する．

In[4]:=

MellinTransform[Cos[x - y^2], {x, y}, {s, t}]

Out[4]=

基本的なメリン変換の表を生成する．

完全なWolfram言語入力を表示する

In[5]:=

flist = {E^(-a x), HeavisideTheta[x - a] x^b, 
      1/(1 + x), Log[1 + x], Sin[x], Cos[x], E^(-x^2), 
  1/(E^x^(-1) x)}; 
Grid[Map[Style[#, ScriptLevel -> 0] &, 
   Join[{{HoldForm@f[x], HoldForm@MellinTransform[f[x], x, s]}}, 
    Transpose[{flist, Map[MellinTransform[#, x, s] &, flist]}]], {2}],
   Dividers -> All, Spacings -> {4, 2}, 
  Background -> {None, {{None, GrayLevel[.9]}}, {{1, 1} -> 
      Hue[.6, .4, 1], {1, 2} -> Hue[.6, .4, 1]}}, 
  BaseStyle -> {FontFamily -> Times, 
    FontSize -> 13}] // TraditionalForm

Out[5]//TraditionalForm=