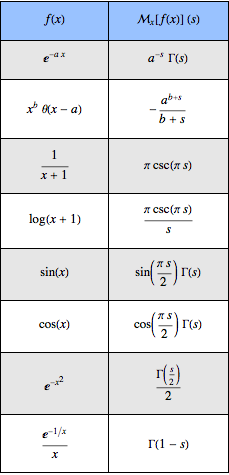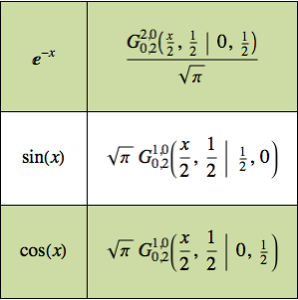Wolfram 언어™

멜린 변환의 계산

MellinTransform을 사용하여 함수의 멜린 변환을 계산합니다.

In[1]:=

MellinTransform[E^(-a x), x, s]

Out[1]=

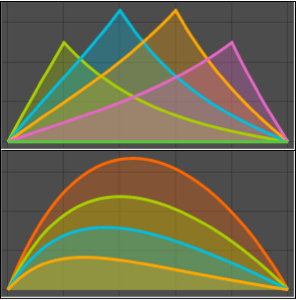
a의 다른 값에 대한 결과를 플롯합니다.

In[2]:=

MellinTransform[E^(-a x), x, s]; Plot[Table[% , {a, 1, 2, 1/4}] // Evaluate, {s, 0, 4}]

Out[2]=

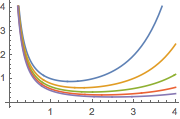
결과의 타당성에 대한 조건을 생성합니다.

In[3]:=

MellinTransform[E^(-a x), x, s, GenerateConditions -> True]

Out[3]=

다변량의 멜린 변환을 계산합니다.

In[4]:=

MellinTransform[Cos[x - y^2], {x, y}, {s, t}]

Out[4]=

기본적인 멜린 변환 테이블을 생성합니다.

In[5]:=

flist = {E^(-a x), HeavisideTheta[x - a] x^b, 1/(1 + x), Log[1 + x], Sin[x], Cos[x], E^(-x^2), 1/(E^x^(-1) x)}; Grid[Map[Style[#, ScriptLevel -> 0] &, Join[{{HoldForm@f[x], HoldForm@MellinTransform[f[x], x, s]}}, Transpose[{flist, Map[MellinTransform[#, x, s] &, flist]}]], {2}], Dividers -> All, Spacings -> {4, 2}, Background -> {None, {{None, GrayLevel[.9]}}, {{1, 1} -> Hue[.6, .4, 1], {1, 2} -> Hue[.6, .4, 1]}}, BaseStyle -> {FontFamily -> Times, FontSize -> 13}] // TraditionalForm

Out[5]//TraditionalForm=