Solve the Tautochrone Problem
The tautochrone problem requires finding the curve down which a bead placed anywhere will fall to the bottom in the same amount of time. Expressing the total fall time in terms of the arc length of the curve and the speed  yields the Abel integral equation
yields the Abel integral equation 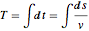 . Defining the unknown function
. Defining the unknown function 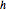 by the relationship
by the relationship 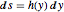 and using the conservation of energy equation
and using the conservation of energy equation 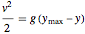 yields the following explicit equation.
yields the following explicit equation.
abeleqn = T == 1/Sqrt[2 g] \!\(
\*SubsuperscriptBox[\(\[Integral]\), \(0\), \(y\)]\(
\*FractionBox[\(h[z]\),
SqrtBox[\(y - z\)]] \[DifferentialD]z\)\);Use DSolveValue to solve the integral equation.
dsdy = DSolveValue[abeleqn, h[y], y]Using the relationship 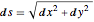 , solve for
, solve for  .
.
dxdy = Sqrt[dsdy^2 - 1]Starting the curve from the origin and integrating yields 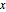 as a function of
as a function of  . Notice that the assumptions ensure the integrand is real valued.
. Notice that the assumptions ensure the integrand is real valued.
x[y_] = Integrate[dxdy, {y, 0, y},
Assumptions -> (2 g (T^2) )/(\[Pi]^2 y) > 1 && y > 0]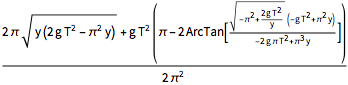
Using a time of descent of two seconds and substituting in the value of the gravitational acceleration, plot the maximal curve for the tautochrone. (The branch 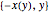 comes from the solution
comes from the solution 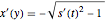 for the derivative of
for the derivative of  .)
.)
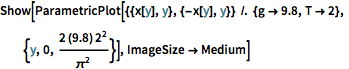
Show[ParametricPlot[{{x[y], y}, {-x[y], y}} /. {g -> 9.8, T -> 2}, {y,
0, (2 (9.8) 2^2)/\[Pi]^2}], ImageSize -> Medium]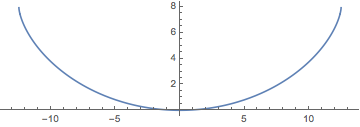
Making the change of variables 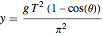 gives a simple, nonsingular parametrization of the curve with
gives a simple, nonsingular parametrization of the curve with 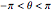 .
.
c[\[Theta]_] = (
g T^2)/\[Pi]^2 {Sin[\[Theta]] + \[Theta], 1 - Cos[\[Theta]]} ;Combining the conservation of energy equation and the chain rule 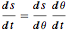 produces the following differential equation for
produces the following differential equation for 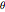 as a function of
as a function of 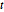 , which can be solved numerically.
, which can be solved numerically.
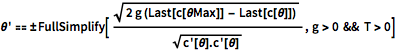
\[Theta]' == \[PlusMinus]FullSimplify[ Sqrt[
2 g (Last[c[\[Theta]Max]] - Last[c[\[Theta]]])] /Sqrt[
c'[\[Theta]].c'[\[Theta]]] , g > 0 && T > 0]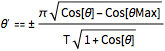
Visualize the motion along the tautochrone.