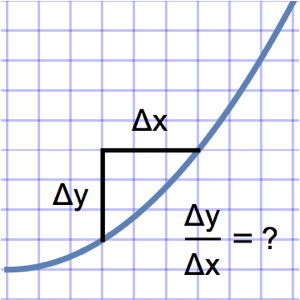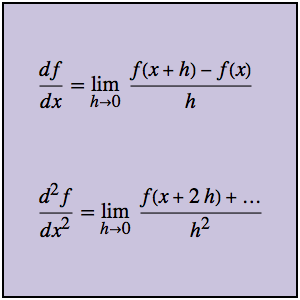Compute Difference Quotients
The Wolfram Language can compute not only the well-known univariate difference quotient, but multivariate and higher-order quotients as well.
In[1]:=
DifferenceQuotient[f[x], {x, h}]Out[1]=
The second-order difference quotient is the difference quotient of the first-order quotient.
In[2]:=
DifferenceQuotient[f[x], {x, 2, h}]Out[2]=
In[3]:=
DifferenceQuotient[f[x], {x, h}];
DifferenceQuotient[f[x], {x, 2, h}];
% == DifferenceQuotient[%%, {x, h}]Out[3]=
Compute a multivariate difference quotient.
In[4]:=
DifferenceQuotient[(x + y + 1)/(((x^2 + 3) (y + 5))), {x, h}, {y, k}]Out[4]=
Create a table of increasing difference quotients of a polynomial, which produces polynomials of decreasing order.
In[5]:=
Grid[Table[
DifferenceQuotient[x^3 y^2 + 5 x y + 11, {x, i, r}, {y, j, s}], {i,
4}, {j, 3}], Spacings -> {2, 1}]Out[5]=