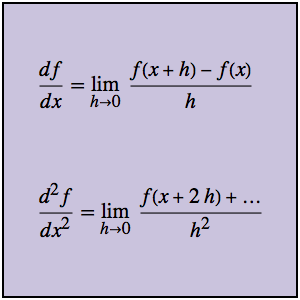Solve a SIAM Challenge Problem

The integral 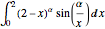depends on the parameter α. Find the value of 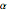that lies between 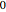and 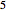and maximizes the integral. The given integral can be regarded as a Mellin convolution of two functions.

In[1]:=

f[x_] := x (2 - x)^\[Alpha] UnitBox[(x - 1)/2]

In[2]:=

g[x_] := Sin[x]

Compute the Mellin convolution of f[x] and g[x].

In[3]:=

(mc = MellinConvolve[f[x], g[x], x, \[Alpha]]) // TraditionalForm

Out[3]//TraditionalForm=

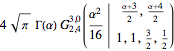
Compare with the result given by Integrate.

In[4]:=

Integrate[(2 - x)^\[Alpha] Sin[\[Alpha]/x], {x, 0, 2}, Assumptions -> \[Alpha] > 0] // TraditionalForm

Out[4]//TraditionalForm=

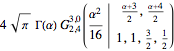
Plot the integral as a function of .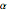

In[5]:=

Plot[mc // Evaluate, {\[Alpha], 0, 4.99}, PlotStyle -> Red]

Out[5]=

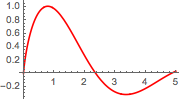
Compute the argument that maximizes the integral in 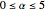using FindArgMax.

In[6]:=

N[FindArgMax[mc, {\[Alpha], 1}, WorkingPrecision -> 100][[1]], 20]

Out[6]=