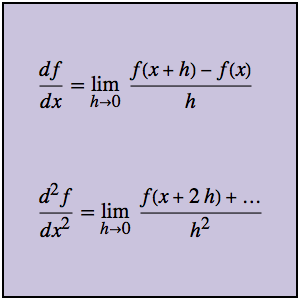求解积分微分方程
解一个积分微分方程.
In[1]:=
eqn = Derivative[1][y][x] == 1 + Sin[a x] + \!\(
\*SubsuperscriptBox[\(\[Integral]\), \(0\), \(x\)]\(y[
t] \[DifferentialD]t\)\);获得通解.
In[2]:=
sol1 = DSolveValue[eqn, y[x], x]Out[2]=
设定一个初始条件从而得到一个特解.
In[3]:=
init = y[0] == -1;In[4]:=
sol2 = DSolveValue[{eqn, init}, y[x], x]Out[4]=
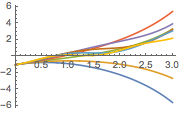
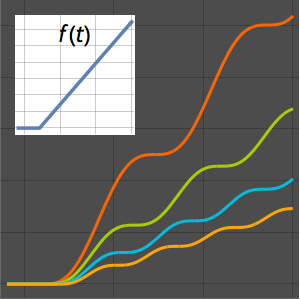
绘制解的曲线.
In[5]:=
Plot[Table[sol2, {a, -1, 4, 0.7}] // Evaluate, {x, 0, 3}]Out[5]=