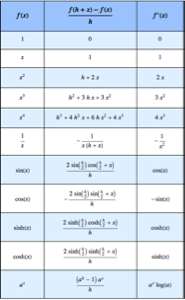
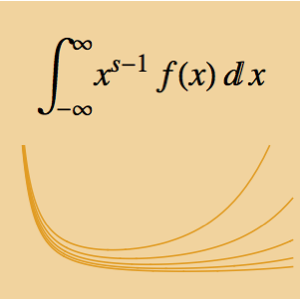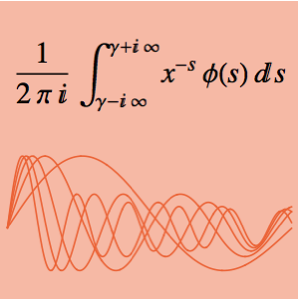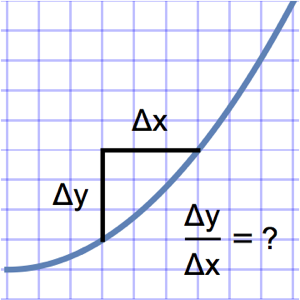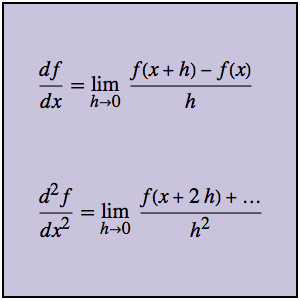Visualisieren Sie Sekanten und Tangenten
Definieren Sie mit DifferenceQuotient die Funktion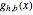 
, die Sekante zwischen 
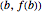und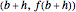 
.
In[1]:=
f[x_] := 10 Exp[-((x^2 - x)/4)] Sin[2 x];In[2]:=
g[h_, b_][x_] =
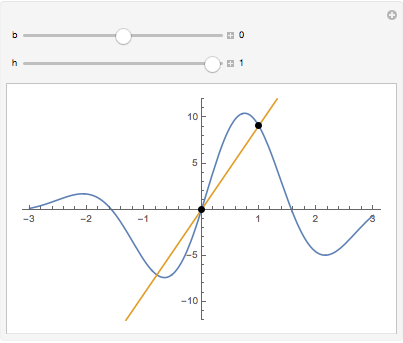
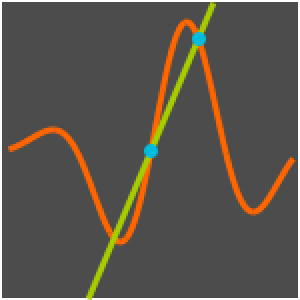
f[b] + (DifferenceQuotient[f[x], {x, h}] /. (x -> b)) (x - b);Visualisieren Sie, wie sich die Sekante bei Verschieben des Basispunkts ändert, sich aber in jedem Basispunkt der Tangente nähert wenn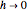 
.
In[3]:=
Manipulate[
Plot[{f[x], g[h, b][x]}, {x, -3, 3}, PlotRange -> 12,
ImageSize -> Medium,
Epilog -> {AbsolutePointSize[7],
Point[{{b, f[b]}, {b + h, f[b + h]}}]}], {{b, 0}, -2, 2,
Appearance -> "Labeled"}, {{h, 1}, -1, 1, Appearance -> "Labeled"}]
